MinimalStateSpaceModel

MinimalStateSpaceModel[sys]

gives the minimal state-space model of the state-space model sys.

MinimalStateSpaceModel[sys,{z1,…}]

specifies the new coordinates zi.

Details and Options

  • The minimal state-space model is both controllable and observable, and has the minimal number of states.
  • The system sys can be a standard or descriptor StateSpaceModel or AffineStateSpaceModel.

Examples

open allclose all

Basic Examples  (1)

Compute a minimal realization:

Scope  (6)

Obtain a model with the minimal number of states:

A minimal realization of a symbolic model:

A minimal realization does not contain uncontrollable modes:

A minimal realization does not contain unobservable modes:

The minimal realization of a descriptor system:

The minimal realization of an affine system:

Specify the new variable:

Applications  (2)

Remove any uncontrollable or unobservable modes:

A parallel mass-spring-damper system is not completely controllable and observable. Design a controller based on the minimal system:

A model of the system:

Compute the minimal model:

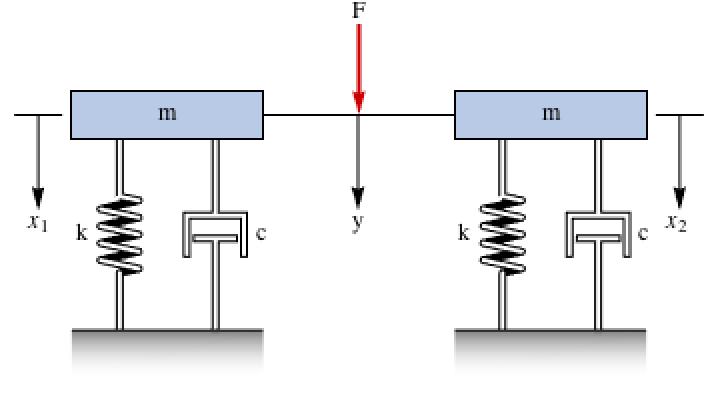
Design a controller based on the minimal system:

The closed-loop system:

Simulate the response of the closed-loop system and compare it with the open-loop system:

Properties & Relations  (4)

MinimalStateSpaceModel computes the subspace that is both controllable and observable:

A minimal realization is both controllable and observable:

Minimal realizations are not unique:

Both are minimal realizations of the same transfer function:

MinimalStateSpaceModel is equivalent to TransferFunctionCancel for scalar systems:

Wolfram Research (2010), MinimalStateSpaceModel, Wolfram Language function, https://reference.wolfram.com/language/ref/MinimalStateSpaceModel.html (updated 2014).

Text

Wolfram Research (2010), MinimalStateSpaceModel, Wolfram Language function, https://reference.wolfram.com/language/ref/MinimalStateSpaceModel.html (updated 2014).

CMS

Wolfram Language. 2010. "MinimalStateSpaceModel." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/MinimalStateSpaceModel.html.

APA

Wolfram Language. (2010). MinimalStateSpaceModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MinimalStateSpaceModel.html

BibTeX

@misc{reference.wolfram_2024_minimalstatespacemodel, author="Wolfram Research", title="{MinimalStateSpaceModel}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/MinimalStateSpaceModel.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_minimalstatespacemodel, organization={Wolfram Research}, title={MinimalStateSpaceModel}, year={2014}, url={https://reference.wolfram.com/language/ref/MinimalStateSpaceModel.html}, note=[Accessed: 18-November-2024 ]}