Minors
詳細

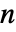 ×
×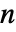 行列に対して,Minors[m]は,第
行列に対して,Minors[m]は,第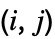

 要素は,m の第
要素は,m の第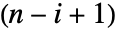
 行と第
行と第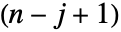

 列を削除することによって得られる行列の行列式を与える. »
列を削除することによって得られる行列の行列式を与える. »- Reverse[Minors[m],{1,2}]は,第
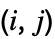

 要素を,m の第
要素を,m の第 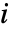 行と第
行と第 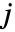
 列の削除に関連付ける. »
列の削除に関連付ける. » - Minors[m]は,Minors[m,Min[Dimensions[m]]-1]に等しい. »
- Minors[m,k]は,m から,k 行と k 列のすべての可能な集合を選ぶことで得られる k×k 部分行列の行列式を与える.
- 得られた結果の要素は,特定の位置のリストの行と列を選ぶことに相当する.要素の順序は,最終の行列を斜めあるいは下方にたどっていくと,位置の連続したリストが辞書順に並ぶようにする.
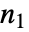 ×
×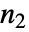 行列に対しては,Minors[m,k]は
行列に対しては,Minors[m,k]は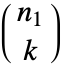 ×
×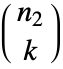 行列を与える.
行列を与える.
例題
すべて開くすべて閉じるスコープ (14)
小行列のサイズ指定 (4)
特殊行列 (4)
アプリケーション (5)
正方行列についてMinors[m]の計算に使われる行列式を可視化する:
m の両方のレベルを反転させて ![]()
![]() 番目の行と
番目の行と ![]()
![]() 番目の列を削除することで
番目の列を削除することで![]()
![]() 番目の項目を得る:
番目の項目を得る:
Adjugateが返す結果と比較する:
階数は,Minors[mat,k]が非零の項を含む最大 k である:
MatrixRankを使って階数が実際に2に等しいことを確かめる:
ハミルトン行列が正定値行列かどうかをシルベスター(Sylvester)の判定法を使って調べる:
すべての首座小行列式が正なので,この行列は正定値行列である:
PositiveDefiniteMatrixQを使って結果を確認する:
特性と関係 (11)
![]() 行列について,Minors[m]は行
行列について,Minors[m]は行 ![]() と列
と列 ![]() を引いて求まる行列式の行列である:
を引いて求まる行列式の行列である:
Reverse[Minors[m],{1,2}]は m から ![]() 行目と
行目と ![]() 列目を削除することで求まる行列式の行列である:
列目を削除することで求まる行列式の行列である:
r=Reverse[Minors[m],{1,2}]とすると,これは![]() として表すことができる:
として表すことができる:
Minors[m]はMinors[m]==Minors[m,Min[Dimensions[m]]-1]に等しい:
正方行列 m について,Minors[m,Length[m]]は{{Det[m]}}に等しい:
デフォルトで,Minors[m,0]は{{1}}である:
MatrixRankより高次元のMinorsは零である:
![]() ×
×![]() 行列の
行列の ![]() 次の小行列式のDimensionsは
次の小行列式のDimensionsは![]() ×
×![]() である:
である:
正方恒等行列のMinorsは別の恒等行列である:
正方対角行列のMinorsは別の対角行列である:
Minorsは実質的に,抽出された行と列の外積に等しい:
テキスト
Wolfram Research (1988), Minors, Wolfram言語関数, https://reference.wolfram.com/language/ref/Minors.html (2022年に更新).
CMS
Wolfram Language. 1988. "Minors." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/Minors.html.
APA
Wolfram Language. (1988). Minors. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Minors.html