MixtureDistribution

MixtureDistribution[{w1,…,wn},{dist1,…,distn}]

表示一种混合分布，其中这种分布的累积分布函数由权重分别为 wi 的分量分布 disti 的累积分布函数之和给出.

更多信息

  • 值 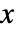的累积分布函数与 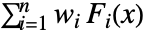成正比，其中 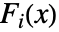是 disti 的累积分布函数.
  • 分布 disti 必须全部连续或全部离散，并且具有相同维数.
  • 权重 wi 可以取任意非负实数.
  • MixtureDistribution 可与 Mean、CDF 以及 RandomVariate 等函数联合使用.

范例

打开所有单元关闭所有单元

基本范例  (3)

定义两个连续分布的混合：

定义两个离散分布的混合：

定义一个多变量混合：

范围  (30)

基本用途  (10)

具有数值权重的正态分布的混合：

累积分布函数：

具有符号权重的正态分布的混合：

概率密度函数：

权重控制了每个分布的影响：

两个单变量连续分布：

混合根据各自的权重将密度合并起来：

两个双变量连续分布：

混合根据各自的权重将密度合并起来：

两个单变量离散分布：

概率密度函数：

绘制不同权重下的密度函数：

均值和方差：

两个多变量离散分布：

概率密度函数：

生成随机数：

几个单变量连续分布：

矩：

阶乘矩：

中心矩：

累积量：

几个单变量离散分布：

母函数：

估计矩中的权重：

参数分布  (5)

定义两个不同的连续分布的混合：

概率密度函数：

风险函数：

在极限情况下，指数分布起主导作用：

定义具有不同支集的两个分布的混合：

对于几个不同的权重值的概率密度函数：

定义两个不同的单变量离散分布的混合：

概率密度函数：

累积分布函数：

可以通过数值得到矩：

定义两个不同的多变量离散分布的混合：

概率密度函数：

协方差：

定义多变量均匀分布的混合分布：

累积分布函数：

非参数分布  (3)

利用 SmoothKernelDistribution 定义一个混合分布：

混合分布根据各个分布的权值将密度合并起来：

利用 EmpiricalDistribution 定义一个混合分布：

混合分布根据各个分布的权值将累积分布函数合并起来：

绘制累积分布函数的曲线：

利用 HistogramDistribution 定义一个混合分布：

混合分布根据各个分布的权值将密度合并起来：

导出分布  (10)

定义一个混合分布，它的分量由 MixtureDistribution 给出：

概率密度函数是分段连续的：

均值是各分量均值的凸组合：

求哪些分量使得混合分布的均值变成不确定的（indeterminate）：

求最小值和最大值的 OrderDistribution 的混合分布：

比较概率密度函数：

混合分布的均值：

与次序分布的均值的平均数比较：

求 TruncatedDistribution 的混合分布：

概率密度函数不是连续的：

可以通过显式计算得到均值：

求利用 ProductDistribution 的混合分布的概率密度函数：

定义利用 TransformedDistribution 的混合分布：

概率密度函数：

定义 MarginalDistribution 的混合分布：

特征函数：

定义利用 CensoredDistribution 的混合分布：

概率密度函数：

利用 ParameterMixtureDistribution 的混合分布：

尺度缩放后的混合分量和混合分布的概率密度函数：

定义利用 CopulaDistribution 的混合分布：

相容的 QuantityDistribution 的混合，计算结果为 QuantityDistribution：

计算出均值：

画出 PDF 的图形：

自动化简  (2)

一个分量混合分布化简为输入分布：

权值为零的混合分布将减少输入分布的数目：

与零权重混合不会被计算：

应用  (7)

求值在 和 之间的百分比：

在 和 之间：

利用 NProbability 将其打包成一个函数：

确定一个混合的最大方差：

在美国女性的身高服从正态分布，平均为 64 英寸、标准差为2英寸，而在美国男性的身高也服从正态分布，平均为 70 英寸、标准差为 2 英寸. 如果男性对女性的人口比例为 1.1，那么整个人口的高度，双峰分布如下：

模拟人口为 100 的小镇的一个典型身高分布：

查找至少 73 英寸高的概率：

在电压信号的二进制传输中，0 表示 伏，1 表示 伏. 发送信号 1 的概率为 ，但信号被白噪声破坏. 求所接受到的信号的概率密度函数：

在 p=0.4 及 v=1 时，模拟接收器处的传输：

要区分两种信号，电压差必须较大：

MixtureDistribution 可以用来创建多峰模型：

在选择的年份中美国地震幅度有两种模式：

从两个正态分布的可能混合求估计分布：

比较直方图和估计分布的概率密度函数：

求地震震级为 7 或更高的概率：

求平均地震震级：

模拟 30 个地震的震级：

中型汽车的城市和高速平均里程数服从一个双正态分布：

显示城市和高速里程数的分布：

假定 65% 的行驶是在城市内的，则里程数服从一个 MixtureDistribution：

求里程数均值：

高斯混合模型常被用在图像分割中. 图像被表示为像素数组. 每个像素是一个表示亮度（或颜色）的标量（或向量）：

用 Histogram 可视化像素值的分布：

用 EstimatedDistribution 把像素值拟合成三个分量的高斯混合分布：

用最大后验概率 (MAP) 估计标注每个像素：

可视化结果：

属性和关系  (8)

权重为 w 的混合等价于权重为 w/Total[w] 的混合：

比较概率密度函数：

一个混合的概率密度函数是其各个分量的概率密度函数的凸组合：

一个混合的累积分布函数是其各个分量的累积分布函数的凸组合：

混合分布的矩是各分量的矩的凸组合：

普通阶的矩：

假定数值数目有限，具有一个离散权值的 ParameterMixtureDistribution 可以表示为一个混合分布：

比较概率密度函数：

假定数值数目可数，具有一个离散权值的 ParameterMixtureDistribution 可以使用混合分布近似：

比较不同分位数作为临界值的近似值：

通过一个混合分布近似一个具有连续权值的 ParameterMixtureDistribution：

比较概率密度函数：

一个 KernelMixtureDistribution 是从数据推导出的一个 MixtureDistribution：

巧妙范例  (3)

两个双正态分布的混合：

高斯混合分布的各种形状：

一个多变量高斯混合：

Wolfram Research (2010)，MixtureDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/MixtureDistribution.html （更新于 2016 年）.

文本

Wolfram Research (2010)，MixtureDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/MixtureDistribution.html （更新于 2016 年）.

CMS

Wolfram 语言. 2010. "MixtureDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/MixtureDistribution.html.

APA

Wolfram 语言. (2010). MixtureDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MixtureDistribution.html 年

BibTeX

@misc{reference.wolfram_2024_mixturedistribution, author="Wolfram Research", title="{MixtureDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MixtureDistribution.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_mixturedistribution, organization={Wolfram Research}, title={MixtureDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/MixtureDistribution.html}, note=[Accessed: 22-November-2024 ]}