ModelPredictiveController

ModelPredictiveController[sspec,cost,cons]

计算系统规范为 sspec 的模型预测控制器，可最小化成本函数 cost 并满足约束条件 cons.

ModelPredictiveController[…,"prop"]

返回属性 "prop" 的值.

更多信息和选项

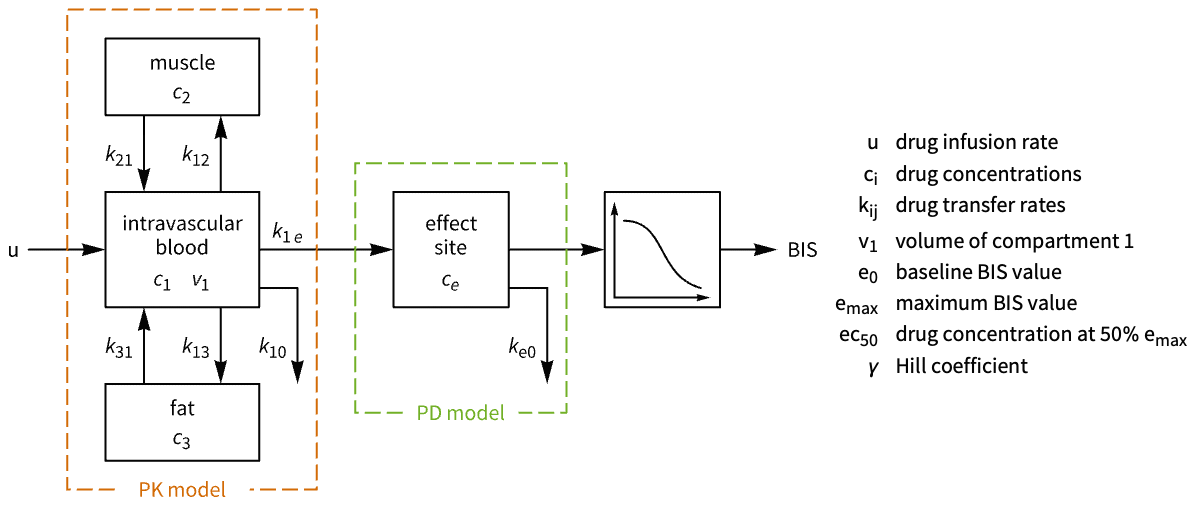
  • 模型预测控制亦称为 MPC.
  • 通过最小化状态的成本函数和在有限时域内控制输入来计算模型预测控制器，同时允许对输入和状态施加约束条件. 这些约束条件通常对于确保安全地实现控制器很重要.
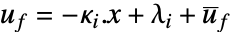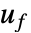  • 所得控制器为简单的分段仿射形式 ，其中 是反馈控制输入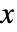， 是系统的状态. 可以很容易地将这些参数部署在微控制器中并用于快速处理.
  • 调节器的目的是在有干扰 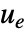将系统推离的情况下使系统保持在平衡位置. 典型的例子包括将倒立摆保持在直立位置或保持飞机水平飞行.
  • MPC 调节器被指定为最小化成本 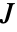的反馈，成本取决于 sspec 中的系统动力学 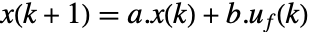和约束条件 cons. 当状态 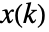和反馈控制输入 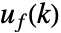都变小时，成本 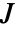变小.
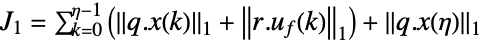
  • 1-norm，加权积分绝对误差 (IAE)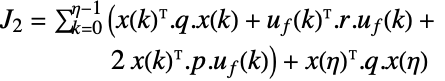
    平方 2-norm，加权积分平方误差 (ISE) 或加权 "energy"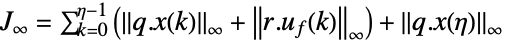
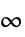    -norm，加权峰值
  • 在 cost Association 中指定成本 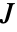，其中有以下键：
  • η"Horizon"整数时域
    q"StateWeight"状态的矩阵成本
    r"InputWeight"输入的矩阵成本
    p"StateInputWeight"交叉耦合的状态和输入的矩阵成本
    m"Norm"1、2 或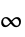
  • 跟踪器的目的是在有干扰 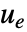存在的情况下跟踪参考信号 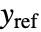. 典型的例子包括汽车的巡航控制系统或机器人的路径跟踪.
  • MPC 跟踪器被指定为最小化成本的反馈，成本取决于 sspec 中的系统动力学 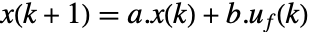和约束条件 cons. 当预测误差 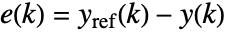和增量反馈控制输入 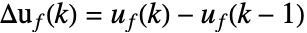都变小时，成本变小.
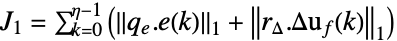
  • 1-norm，加权积分绝对误差 (IAE)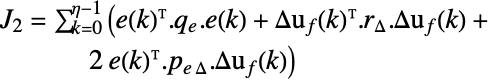
    平方 2-norm，加权积分平方误差 (ISE) 或加权 "energy"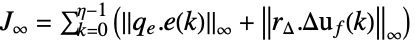
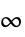    -norm，加权峰值
  • 成本函数表达式中的项如下：
  • η"Horizon"整数时域
    qe"ErrorWeight"误差的矩阵成本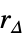
    r_Delta"InputIncrementWeight"输入增量的矩阵成本
    peΔ"ErrorInputIncrementWeight"交叉耦合的误差和输入增量的矩阵成本
    m"Norm"1、2 或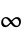
  • 调节器和跟踪器问题的约束条件 cons 是用状态变量 x、输入变量 u 和输出变量 y 表示的. 可用 StateSpaceModel[{a,b,c,d},x,u,y,…] 来定义.
  • 对于特定时刻 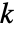成立的约束条件，其中 ：
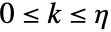  • xmin<=xi[k]<=xmax对时间 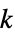上的值的约束条件
    Δxmin<=xi[k2]-xi[k1]<=Δxmax对从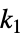时间 到时间 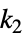的增量的约束条件
  • 对所有时刻 k 成立的约束条件，其中 ：
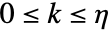  • xmin<=xi<=xmax对所有 k 上的值的约束条件
    min<=α1.x1+…+αn.xn+β<=max对所有 k 的线性组合的约束条件
    xminxxmax对所有 k 的所有值的约束条件
  • 可按以下形式指定权重矩阵 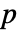、 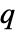和 ：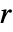
  • q常数权重 {q,…,q,q}
    {{q},qη}不同的最终权重 {q,…,q,qη}
    {q0,q1,…,qη}不同的权重 {q0,q1,…,qη}
  • ModelPredictiveController 适用于可以用 StateSpaceModel[…,SamplingPeriodτ] 指定的离散时间线性系统.
  • 系统规范 sspec 可以采用以下形式：
  • StateSpaceModel[…]线性控制输入和线性状态
    AffineStateSpaceModel[…]线性控制输入和非线性状态
    NonlinearStateSpaceModel[…]线性控制输入和非线性状态
    SystemModel[…]一般系统模型
    <|…|>以 Association 给出的详细的系统规范
  • 详细的系统规范可以含有以下键：
  • "InputModel"sys任意一个模型
    "FeedbackInputs"All反馈输入 uf
    "TrackedOutputs"None跟踪的输出 yref
  • 反馈输入可以采用以下形式：
  • {num1,…,numn}StateSpaceModel、AffineStateSpaceModel 和 NonlinearStateSpaceModel 使用的编号输入 numi
    {name1,…,namen}SystemModel 使用的已命名输入 namei
    All使用所有输入
  • ModelPredictiveController 返回一个 SystemsModelControllerData 对象 cd，可通过形式 cd["prop"] 提取其他属性.
  • ModelPredictiveController[…,"prop"] 可用于直接获取 cd["prop"] 值.
  • 闭环系统的属性：
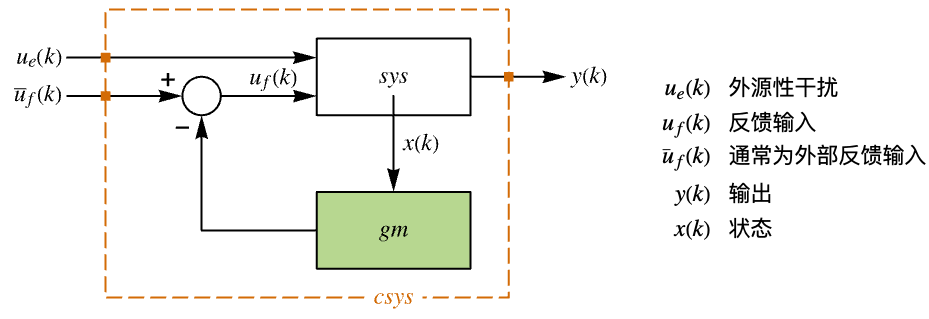
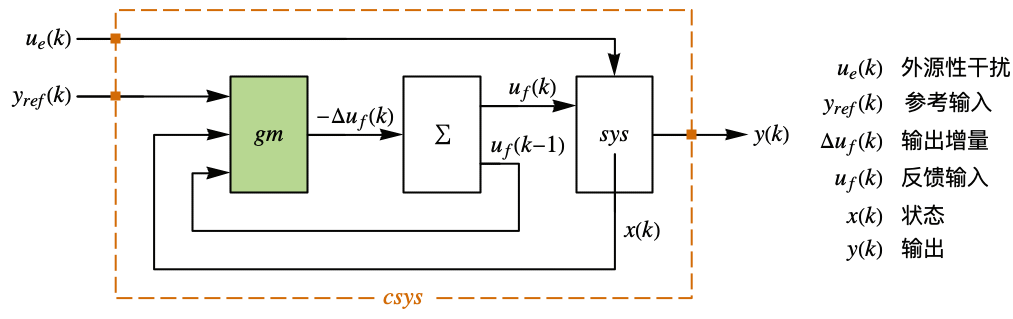
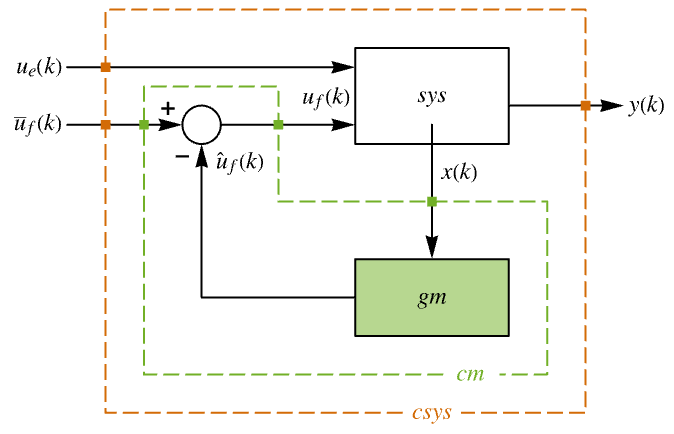
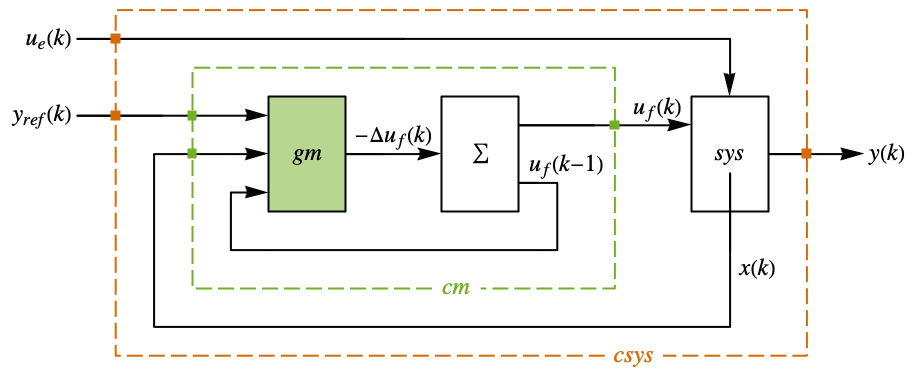
  • "ClosedLoopPoles"线性化 "ClosedLoopSystem" 的极点
    "ClosedLoopSystem"系统 csys
    {"ClosedLoopSystem", cspec}对闭环系统形式的具体控制
    "ControllerModel"模型 cm
    "FeedbackGains"增益矩阵 κ 或其等价形式
    "FeedbackGainsModel"模型 gm
    "FeedbackRegions"反馈可行的区域
    "QuasiClosedLoopSystem"用 "QuasiFeedbackGains" 组合起来的闭环
    "QuasiFeedbackGains"只依赖于初值的反馈增益
    "QuasiFeedbackGainsModel""QuasiFeedbackGains" 的系统模型
    "OptimalCost" 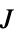的最优值
  • 无限时域问题的属性：
  • "MaximalLQRInvariantRegion"含有 LQR 反馈增益的最大区域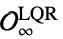
    "MaximalStabilizableRegion"可以进入 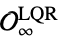的最大区域 K_infty TemplateBox[{{(, O}, infty, LQR}, Subsuperscript])
    "MinimalFiniteHorizon"K_infty TemplateBox[{{(, O}, infty, LQR}, Subsuperscript]) 中的状态进入 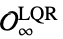的最小时域
  • 基本设计的属性：
  • "Design"控制器设计的类型
    "DesignModel"设计所用的模型
    "DesignModelSamplingMethod"用来获取 "DesignModel" 的采样方法
    "DesignModelSamplingPeriod""DesignModel" 的采样周期
    "Horizon"时域 η
    "Norm"1-、平方 2- 或 ∞-norm
  • 输入模型的属性：
  • "FeedbackInputs"用于反馈的 sys 的输入 uf
    "InputModel"输入模型 sys
    "InputsCount"sys 的输入 u 的数量
    "OpenLoopPoles""DesignModel" 的极点
    "OutputsCount"sys 的输出 y 的数量
    "SamplingPeriod"sys 的采样周期
    "StatesCount"sys 的状态 x 的数量
    "TrackedOutputs"sys 被跟踪的输出 yt

    • 调节器的结构图.

    跟踪器的结构图.

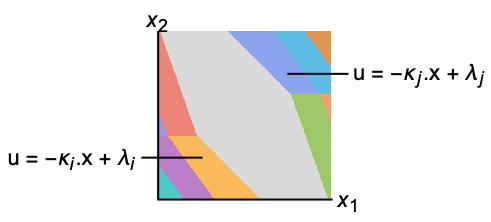
范例

打开所有单元关闭所有单元

基本范例  (2)

求解状态为 {x1,x2}、控制输入为 u 的系统的无限时域调节器问题：

指定代价为 ：

状态和输入约束条件：

计算所得的 MPC 控制器：

闭环系统：

具有可行反馈的区域：

可行区域内从不同初始点开始的闭环系统仿真：

求解状态为 {x1,x2}、控制输入为 u 的系统的有限时域调节器问题：

指定代价为 ：

状态和输入约束条件：

计算所得的 MPC 控制器：

闭环系统：

闭环系统对输入序列的响应：

准闭环系统：

准闭环系统对输入序列的响应：

范围  (43)

基本用法  (5)

求解状态为 {x1,x2}、控制输入为 u 的离散时间系统的调节器问题：

最小化 ：

限制状态 ，控制输入 ：

计算控制器：

闭环系统：

闭环系统的响应：

上面的闭环系统：

它由输入模型、反馈增益和比较器组成：

子系统的阶数：

从非零初始条件开始仿真闭环系统：

从不同的初始条件开始：

输入为 {u1,u2} 的多输入系统：

成本：

约束条件：

计算控制器：

控制器是一个 DiscreteInputOutputModel：

本质上是一组分段函数：

并有两个状态作为输入：

采样周期为 0.1 的系统：

成本：

约束条件：

计算控制器：

输出响应：

绘制采样时刻的响应：

将其绘制为时间的函数：

上面的控制器数据对象：

先获取控制器的模型和闭环系统，然后计算控制器的工作量：

对输入序列的输出响应：

控制范围为 的情况下控制器的工作量：

范数  (4)

设计一个使 1 范数成本最小化的控制器：

控制器是一个 DiscreteInputOutputModel：

它是一组分段函数：

设计一个使 范数成本最小化的控制器：

控制器是一个 DiscreteInputOutputModel：

是一组分段函数：

设计一个使平方 2 范数成本最小化的控制器：

控制器是一个 DiscreteInputOutputModel：

是一组分段函数：

设计一个控制器，使无限时域的平方 2 范数成本最小化：

控制器是一个 NonlinearStateSpaceModel：

没有状态变量：

是输入模型状态的分段函数：

跟踪  (4)

求解状态为 {x1,x2}、控制输入为 u 的离散时间系统的跟踪问题：

成本：

约束条件：

计算跟踪控制器：

闭环系统：

闭环响应：

上面的闭环系统：

它对非恒定类阶跃参考信号的响应：

响应没有超过上限 5：

对正弦参考信号的响应：

比较对不同范数的响应：

不同范数情况下的控制器：

闭环系统：

响应：

1-范数和 -范数的响应是相同的，因为它是一个单入单出系统：

2-范数和 1-范数响应的误差范数：

比较多输出系统的范数：

针对不同范数的成本指定：

控制器：

闭环系统：

响应：

1-范数和 -范数成本响应之差：

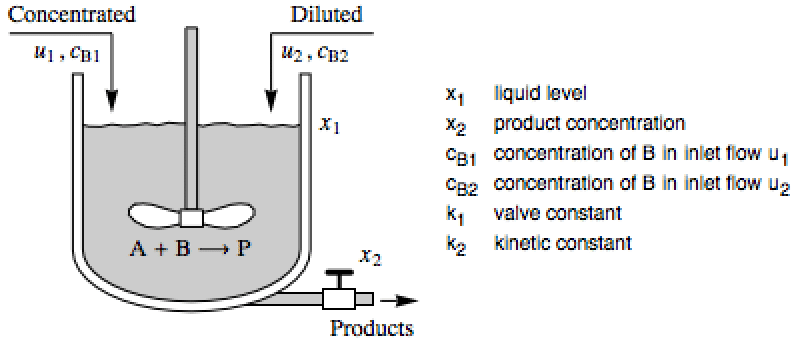
工厂模型  (8)

由 StateSpaceModel 指定的系统的控制器：

由 AffineStateSpaceModel 指定的系统：

控制器：

它是基于线性近似计算的：

反馈增益相同：

具有非零工作点的非线性系统：

控制器：

它是基于线性近似计算的：

非零工作点导致增益不同：

由 NonlinearStateSpaceModel 指定的系统的控制器：

由连续时间 SystemModel 指定的系统：

完整的系统规范还包括采样：

成本：

由形式变量指定的约束条件：

控制器：

有时也可以用变量的标签指定约束条件：

控制器：

反馈增益相同：

具有反馈和外源性输入的系统：

完整的系统规范：

成本只包含反馈输入成本：

约束条件只包括对反馈输入的约束条件：

控制器：

反馈增益模型有两个状态 {x1,x2} 作为输入，u1 为输出：

具有多个输出的系统：

只跟踪第一个输出的完整系统规范：

成本只包括跟踪输出的误差：

约束条件：

控制器：

只跟踪第一个输出：

具有多个输入的 SystemModel：

用变量名指定的反馈输入：

反馈输入索引：

是线性化 StateSpaceModel 的第一个输入：

约束条件  (5)

用逻辑表达式指定的约束条件：

用列表指定的约束条件：

用向量和标量不等式指定的约束条件：

为特定 指定的约束条件：

包括控制率的约束条件：

计算控制器的数据：

闭环系统的响应：

控制器的工作量：

控制率在范围 内：

属性  (17)

可从控制器数据对象计算可用属性列表：

可以直接计算特定属性：

还可以计算属性列表：

反馈增益：

它是一组分段函数：

状态上是仿射的：

可用于计算反馈增益模型：

直接获取反馈增益模型：

可用于计算控制器模型：

和闭环系统：

最优成本：

它是三个分段函数的总和：

在每个时刻都是最优成本：

并且是二次的：

从最小时刻到最大时刻排序：

每个时刻的最优成本是分段二次的：

1-范数问题的最优成本：

每个时刻的最优成本是分段线性的：

-范数问题的最优成本：

每个时刻的最优成本是分段线性的：

-时域问题的最优成本：

它是分段二次的：

-时域问题中感兴趣的区域：

"MaximalLQRInvariantRegion" 被包含在 "MaximalStabilizableRegion" 中：

"MaximalStabilizableRegion" 本质上与 "FeedbackRegions" 相同：

"FeedbackRegions" 由多个凸子区域组成：

"MaximalStabilizableRegion" 是单个凸区域：

-时域问题的闭环极点是分段函数：

有限时域问题的闭环极点是一组分段函数：

准反馈增益：

它们是分段函数：

这只取决于系统的初始状态：

准反馈增益模型：

它是根据准反馈增益计算得出的：

准闭环系统：

它是根据准反馈增益模型计算得出的：

基本设计属性：

输入模型属性：

以 Association 的形式获取所有属性：

或是 Dataset：

应用  (2)

设计一个控制器来自动对患者进行麻醉： »

药代动力学 (PK) 特征模型：

药效学 (PD) 特征模型：

使用希尔方程的双谱指数 (BIS) 和 之间关系的模型：

显示希尔方程非线性特征的图：

以 为输入、 为输出的间隔模型：

模型的离散时间近似：

设置成本以跟踪输出：

计算完全清醒和中度清醒但不是深度昏睡的 BIS 值的 ：

指定约束条件以防止患者进入深度昏睡状态：

计算控制器：

闭环系统：

计算使 BIS 值为 的 ，可使患者进入中等昏睡状态：

自动化过程的 图：

BIS 图：

设计一个控制器来改进等温连续搅拌罐反应器过程：»

状态为 、输入为 的系统模型：

计算模型的离散时间近似：

开环系统的响应：

设计一个 MPC 控制器：

闭环系统：

闭环系统的响应：

比较开环和闭环响应：

控制器的工作量：

属性和关系  (3)

LQRegulatorGains 是平方 2-范数无限时域问题的特例：

没有约束条件的 ModelPredictiveController 给出了基本相同的结果：

LQRegulatorGains 不考虑约束条件：

ModelPredictiveController 考虑状态和控制约束条件：

因此 LQRegulatorGains 只有一组反馈增益：

而 ModelPredictiveController 的反馈增益是分段函数：

还可以计算反馈可行的区域：

计算可行区域的边界：

从 （在可行区域之外）开始仿真 LQR 闭环系统：

违反了控制约束条件 ：

含有 MPC 控制器的闭环系统从不可行的初始值 开始的响应：

LQR 和 MPC 闭环系统从可行初始值 开始的响应：

控制器响应表明 LQR 控制器再次违反了控制约束条件：

通过求解多个多参数优化问题来计算 MPC 控制器：

计算二次成本的函数：

形成约束条件的函数：

组合变量的函数：

针对各种情况下的实例求解优化问题：

ModelPredictiveController 给出了基本相同的结果：

可能存在的问题  (2)

不支持 -时域情况下的 1-、-范数问题：

将其改为平方 2-范数问题：

或有限时域问题：

时域问题的约束条件不能包含 和 项：

用状态和输入变量指定约束条件：

或者使时域有限：

Wolfram Research (2022)，ModelPredictiveController，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ModelPredictiveController.html.

文本

Wolfram Research (2022)，ModelPredictiveController，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ModelPredictiveController.html.

CMS

Wolfram 语言. 2022. "ModelPredictiveController." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ModelPredictiveController.html.

APA

Wolfram 语言. (2022). ModelPredictiveController. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ModelPredictiveController.html 年

BibTeX

@misc{reference.wolfram_2024_modelpredictivecontroller, author="Wolfram Research", title="{ModelPredictiveController}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/ModelPredictiveController.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_modelpredictivecontroller, organization={Wolfram Research}, title={ModelPredictiveController}, year={2022}, url={https://reference.wolfram.com/language/ref/ModelPredictiveController.html}, note=[Accessed: 18-November-2024 ]}