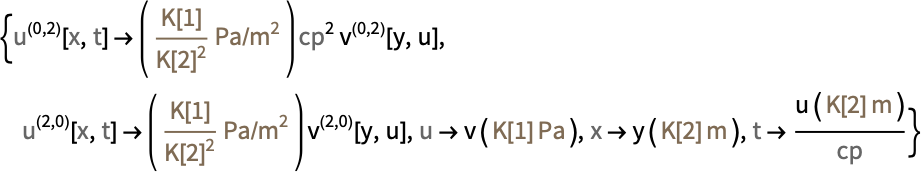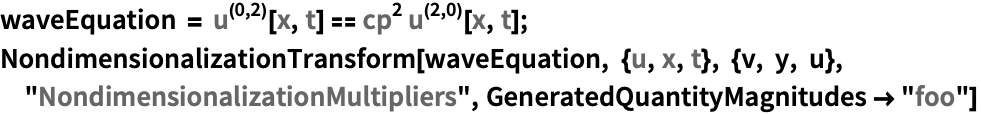WOLFRAM

Wolfram言語 ＆ システム ドキュメントセンター
Wolfram言語ホームページ »

NondimensionalizationTransform
✖
NondimensionalizationTransform

✖

もとの変数 ovars を変数 fvars で置換することで eq を無次元化する．

✖
NondimensionalizationTransform[eq,ovars,fvars,prop]

eq の無次元化に関連する特性を返す．

詳細とオプション

  • eq は，QuantityオブジェクトとQuantityVariableオブジェクトから構築された方程式または微分方程式，またはそのような式のリストである．
  • ovars は eq 中に存在するQuantityVariableオブジェクトのリストである．
  • fvars は ovar のための置換変数のリストである．
  • NondimensionalizationTransformは，無次元方程式に加え，有次元形式から無次元形式への「前進」変換および新たな無次元形式をもとの方程式に戻す「逆」変換のための規則を与えることができる．
  • NondimensionalizationTransformは次の特性をサポートする．
  • "DimensionalizationMultipliers"逆変換のための乗数のAssociation
    "DimensionalizationRules"変換を戻すための規則のリスト
    "NondimensionalizationMultipliers"変換された変数のための乗数のAssociation
    "NondimensionalizationRules"方程式を無次元化するための規則のリスト
    "ReducedForm"無次元化された方程式
  • あるいは，"PropertyAssociation"を使って特性のAssociationを返すことができる．
  • NondimensionalizationTransformは，デフォルトで，"ReducedForm"を返す．
  • 次は，使用可能なオプションである．
  • GeneratedParameters C生成された置換変数の名付け方
    GeneratedQuantityMagnitudes K生成された数量因子の名付け方
    IncludeQuantities {}含める追加的な数量
    UnitSystem Automatic因子を生成するために使われる単位系
  • QuantityVariableオブジェクトとQuantityオブジェクトを使って方程式内の変数からすべての次元を削除することが不可能な場合は，GeneratedQuantityMagnitudes設定が使われる．その場合には，GeneratedQuantityMagnitudesオプションで与えられた記号と一緒に新たな数量が解に加えられる．
  • ovar には含まれていない方程式内に追加的なQuantityVariableオブジェクトがある場合は，GeneratedParameters設定が使われる．NondimensionalizationTransformは方程式からすべてのQuantityVariableオブジェクトを削除する．追加的なQuantityVariableオブジェクトはGeneratedParametersオプションで指定された変数で置換される．
  • IncludeQuantitiesは，無次元解の生成に使う追加的なQuantityオブジェクトを加える．
  • UnitSystemは，方程式から次元を削除する際に乗法因子の生成に使用する単位系を制御する．Automaticのときは，NondimensionalizationTransformが，方程式中に存在する，あるいはIncludeQuantitiesで指定された，単位と物理量から因子を作成する．
  • UnitSystemは自然単位系を使用するように設定することもできる．このオプションには，"DeSitterUnits"，"GaussianNaturalUnits"，"GaussianQuantumChromodynamicsUnits"，"HartreeAtomicUnits"，"LorentzHeavisideNaturalUnits"，"LorentzHeavisideQuantumChromodynamicsUnits"，"PlanckUnits"，"RydbergAtomicUnits"，"StonyUnits"がある．

例題

すべて開くすべて閉じる

例  (2)基本的な使用例

駆動振動方程式から次元を除去する：

In[1]:=1
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-64ig12
Out[1]=1

無次元形式を与える波動方程式の置換規則を計算する：

In[1]:=1
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-vuoiai
In[2]:=2
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-vyttvf
Out[2]=2

スコープ  (4)標準的な使用例のスコープの概要

量子調和振動子の無次元形式について解く：

In[1]:=1
✖
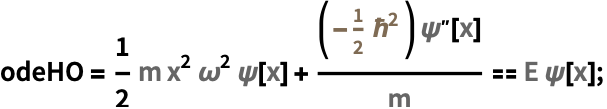
https://wolfram.com/xid/0mfgou7zws85yszseq-ljjkr0
In[2]:=2
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-bl44ji
Out[2]=2

この変換の置換規則を調べる：

In[3]:=3
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-jcgjrt
Out[3]=3

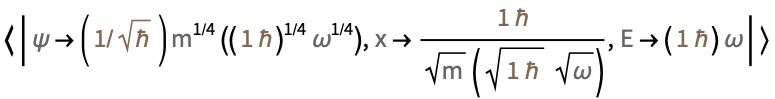
解のC[1]を置換するためのエネルギーの置換変数を指定する：

In[4]:=4
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-t2phuo
Out[4]=4

代数方程式を無次元化する：

In[1]:=1
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-502xrn
In[2]:=2
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-gdsrii
Out[2]=2

RCとLRCの駆動回路についての解を調べる：

In[1]:=1
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-lc4e46
In[2]:=2
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-3swlu8
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-6jog8y
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-6cgjdj
Out[4]=4

この変換の全特性を計算する：

In[5]:=5
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-yssboh
Out[5]=5

LRC回路の無次元化を調べる：

In[6]:=6
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-4y7hy7
Out[6]=6

方程式のリストから次元を一度に削除する：

In[1]:=1
✖
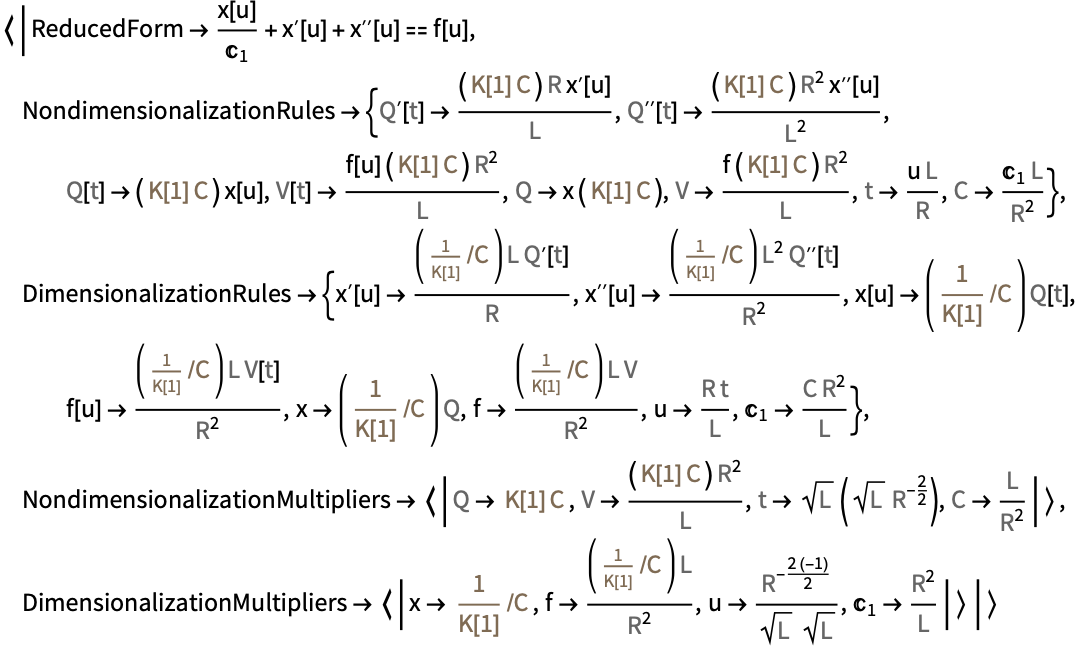
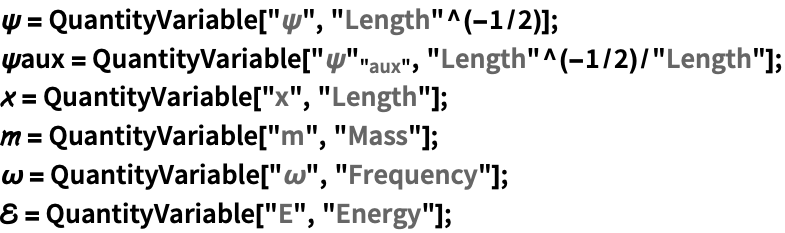
https://wolfram.com/xid/0mfgou7zws85yszseq-x7kuul
In[2]:=2
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-7luxl
In[3]:=3
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-etjicj
Out[3]=3

オプション  (5)各オプションの一般的な値と機能

GeneratedParameters  (1)

導入されたパラメータの名付け方を制御する：

In[1]:=1
✖
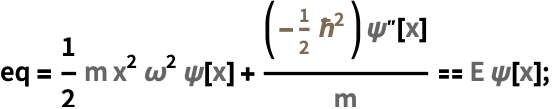
https://wolfram.com/xid/0mfgou7zws85yszseq-q23lfk
In[2]:=2
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-ctxglk
Out[2]=2

より多くのQuantityVariableオブジェクトについての置換を指定することで，GeneratedParametersを完全に回避する：

In[3]:=3
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-49ci0d
Out[3]=3

GeneratedQuantityMagnitudes  (1)

導入された定数の名前を調整する：

In[1]:=1
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-ndasg1
Out[1]=1

あるいは，無次元形式について解くために含める追加的な数量を指定する：

In[2]:=2
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-5go3ps
Out[2]=2

IncludeQuantities  (1)

無次元形式について解くために使える追加的な数量を加える：

In[1]:=1
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-s5ol41
Out[1]=1

UnitSystem  (2)

プランク(Planck)単位系を使ってニュートンの重力法則を簡約する：

In[1]:=1
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-jsq76c
In[2]:=2
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-5fk0th
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-x21rf6
Out[3]=3

標準的なメソッドによる解と比較する：

In[4]:=4
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-3t92ch
Out[4]=4

使用可能な自然単位系と各単位の値を見てみよう：

In[1]:=1
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-uoi9ng
Out[1]=1

アプリケーション  (4)この関数で解くことのできる問題の例

重力についてのポアソン(Poisson)方程式を無次元化する：

In[1]:=1
✖
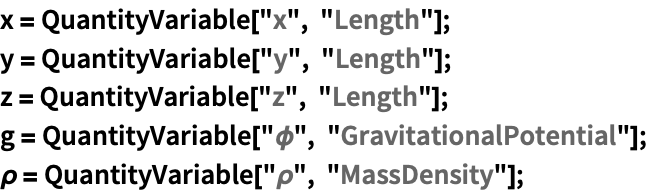
https://wolfram.com/xid/0mfgou7zws85yszseq-gvb9bx
In[2]:=2
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-fs49aj
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-lidlaq
Out[3]=3

無次元のクライン・ゴルドン(Klein–Gordon)方程式を調べる：

In[1]:=1
✖
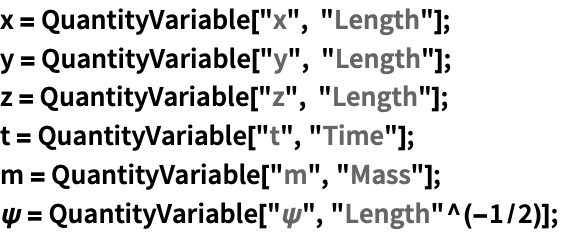
https://wolfram.com/xid/0mfgou7zws85yszseq-cz5ob2
In[2]:=2
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-t0q44o
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-08in1p
Out[3]=3

QuantityVariableオブジェクトの多くについて置換変数を指定することで，結果をさらに簡約する：

In[4]:=4
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-pwk6rh
Out[4]=4

物理系の無次元形式を計算する：

In[1]:=1
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-hpsqpo
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-45xdfi
Out[2]=2

プランク単位系とハートリー(Hartree)単位系を使って，一次元シュレディンガー(Schrödinger)方程式を無次元化する：

In[1]:=1
✖
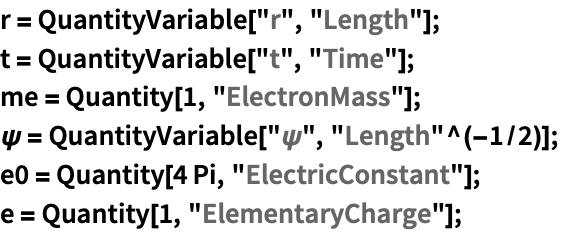
https://wolfram.com/xid/0mfgou7zws85yszseq-bfwdvt
In[2]:=2
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-8k1xy
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-79ugcf
Out[3]=3

結果を調べて無次元であることを確かめる：

In[4]:=4
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-fuk9ci
Out[4]=4

ハートリー原子単位系の解と比較する：

In[5]:=5
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-gscxbj
Out[5]=5

特性と関係  (1)この関数の特性および他の関数との関係

DimensionalCombinationsは，QuantityVariableオブジェクトの無次元の組合せを導出する：

In[1]:=1
✖
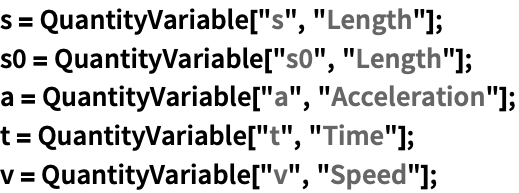
https://wolfram.com/xid/0mfgou7zws85yszseq-yswl2s
In[2]:=2
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-o0vs1w
Out[2]=2

直線運動についての方程式の無次元化規則と比較する：

In[3]:=3
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-x2uyic
In[4]:=4
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-6z2rsr
Out[4]=4

考えられる問題  (3)よく起る問題と予期しない動作

方程式の次元はバランスが取れていなければならない：

In[1]:=1
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-r95tf5
In[2]:=2
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-sqv7bf
Out[2]=2

置換変数は無次元でなければならない：

In[1]:=1
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-rzl3rw
Out[1]=1

与えられた変数は方程式の中になければならない：

In[1]:=1
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-8cxq9k
Out[1]=1

おもしろい例題  (1)驚くような使用例や興味深い使用例

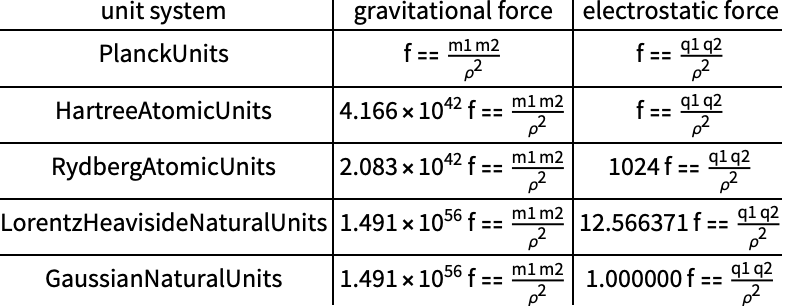
自然単位のさまざまな集合を使った，クーロン(Coulomb)の法則とニュートンの重力法則を変換する：

In[1]:=1
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-lm1ltr
In[2]:=2
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-jd3zk6
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-s2b43n
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-nyfh3n

さまざまな自然単位形で式がどのように見えるかを比較する：

In[5]:=5
✖
https://wolfram.com/xid/0mfgou7zws85yszseq-n44qpa
Out[5]=5
Wolfram Research (2018), NondimensionalizationTransform, Wolfram言語関数， https://reference.wolfram.com/language/ref/NondimensionalizationTransform.html.
✖
Wolfram Research (2018), NondimensionalizationTransform, Wolfram言語関数， https://reference.wolfram.com/language/ref/NondimensionalizationTransform.html.

テキスト

Wolfram Research (2018), NondimensionalizationTransform, Wolfram言語関数， https://reference.wolfram.com/language/ref/NondimensionalizationTransform.html.

✖
Wolfram Research (2018), NondimensionalizationTransform, Wolfram言語関数， https://reference.wolfram.com/language/ref/NondimensionalizationTransform.html.

CMS

Wolfram Language. 2018. "NondimensionalizationTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NondimensionalizationTransform.html.

✖
Wolfram Language. 2018. "NondimensionalizationTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NondimensionalizationTransform.html.

APA

Wolfram Language. (2018). NondimensionalizationTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NondimensionalizationTransform.html

✖
Wolfram Language. (2018). NondimensionalizationTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NondimensionalizationTransform.html

BibTeX

@misc{reference.wolfram_2025_nondimensionalizationtransform, author="Wolfram Research", title="{NondimensionalizationTransform}", year="2018", howpublished="\url{https://reference.wolfram.com/language/ref/NondimensionalizationTransform.html}", note=[Accessed: 07-May-2025 ]}

✖
@misc{reference.wolfram_2025_nondimensionalizationtransform, author="Wolfram Research", title="{NondimensionalizationTransform}", year="2018", howpublished="\url{https://reference.wolfram.com/language/ref/NondimensionalizationTransform.html}", note=[Accessed: 07-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_nondimensionalizationtransform, organization={Wolfram Research}, title={NondimensionalizationTransform}, year={2018}, url={https://reference.wolfram.com/language/ref/NondimensionalizationTransform.html}, note=[Accessed: 07-May-2025 ]}

✖
@online{reference.wolfram_2025_nondimensionalizationtransform, organization={Wolfram Research}, title={NondimensionalizationTransform}, year={2018}, url={https://reference.wolfram.com/language/ref/NondimensionalizationTransform.html}, note=[Accessed: 07-May-2025 ]}