OrthogonalMatrix

converts the orthogonal matrix omat to a structured array.

Details and Options

Orthogonal matrices, when represented as structured arrays, allow for a convenient specification and more efficient operations, including Inverse and LinearSolve.
Matrix decompositions that use orthogonal matrices include QR, Hessenberg, Schur and singular value decompositions.
For an orthogonal matrix 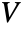, the column vectors 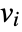are orthonormal so that $v_i.v_j=TemplateBox[{{i, ,, j}}, KroneckerDeltaSeq]$ .

A square orthogonal matrix 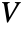is a matrix whose transpose is equal to its inverse; that is, it satisfies the relation .
The inverse of a square orthogonal matrix is also orthogonal.
A matrix 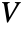of dimensions p×q is orthogonal if p≥q and is the q×q identity matrix, or p≤q and is the p×p identity matrix.
Orthogonal matrices are closed under matrix multiplication, so 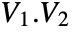is again an orthogonal matrix.
For an OrthogonalMatrix sa, the following properties "prop" can be accessed as sa["prop"]:

	"Matrix"	orthogonal matrix, represented as a full array
	"Properties"	list of supported properties
	"Structure"	type of structured array
	"StructuredData"	internal data stored by the structured array
	"StructuredAlgorithms"	list of functions with special methods for the structured array
	"Summary"	summary information, represented as a Dataset

Normal[OrthogonalMatrix[…]] gives the orthogonal matrix as an ordinary matrix.
OrthogonalMatrix[…,TargetStructure->struct] returns the orthogonal matrix in the format specified by struct. Possible settings include:

	Automatic	automatically choose the representation returned
	"Dense"	represent the matrix as a dense matrix
	"Structured"	represent the matrix as a structured array

OrthogonalMatrix[…,TargetStructureAutomatic] is equivalent to OrthogonalMatrix[…,TargetStructure"Structured"].

Examples

open allclose all

Basic Examples (1)

Construct an orthogonal matrix:

Show the elements:

Normal can convert an OrthogonalMatrix to its ordinary representation:

Scope (5)

Matrices corresponding to isometric transformations (reflections and rotations) are orthogonal:

Real reflection matrices are both orthogonal and symmetric:

A complex orthogonal matrix:

The matrix is orthogonal, but not unitary:

A rectangular orthogonal matrix:

Its transpose is also orthogonal:

OrthogonalMatrix objects include properties that give information about the matrix:

The "Summary" property gives a brief summary of information about the matrix:

The "StructuredAlgorithms" property lists the functions that have structured algorithms:

Options (1)

TargetStructure (1)

Return the orthogonal matrix as a dense matrix:

Return the orthogonal matrix as a structured array:

Applications (5)

Matrices drawn from CircularRealMatrixDistribution are orthogonal:

A rotation matrix:

Orthogonal matrices preserve the standard inner product on $TemplateBox[{}, Reals]^n$ . In other words, if is orthogonal and and are vectors, then :

This means the angles between the vectors are unchanged:

Since the norm is derived from the inner product, norms are preserved as well:

Any orthogonal matrix represents a rotation and/or reflection. If the matrix has determinant , it is a pure rotation. If it the determinant is , the matrix includes a reflection. Consider the following matrix: