WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

PIDDerivativeFilter
✖
PIDDerivativeFilter

✖

is an option to PIDTune that controls the filtering used for derivative terms.

Details

  • The derivative filter replaces the direct derivative 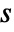with its filtered version 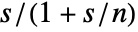, effectively series connecting a lowpass filter with the derivative.
  • The derivative filter 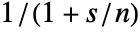is a first-order system with a pole at 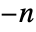. A large 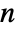value means a fast filter and less filtering effect.
  • Possible settings include:
  • None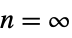, no filtering
    nexplicitly specified filter

Examples

Basic Examples  (1)Summary of the most common use cases

Specify a derivative filter parameter for a PD controller and extract the controller transfer function:

In[1]:=1
✖
https://wolfram.com/xid/0b7e9ckw00yq6fje-dcsuek
In[2]:=2
✖
https://wolfram.com/xid/0b7e9ckw00yq6fje-08w6gk
Out[2]=2

Set the derivative filter of a PID controller:

In[3]:=3
✖
https://wolfram.com/xid/0b7e9ckw00yq6fje-v5b2gz
Out[3]=3
Wolfram Research (2012), PIDDerivativeFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/PIDDerivativeFilter.html.
✖
Wolfram Research (2012), PIDDerivativeFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/PIDDerivativeFilter.html.

Text

Wolfram Research (2012), PIDDerivativeFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/PIDDerivativeFilter.html.

✖
Wolfram Research (2012), PIDDerivativeFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/PIDDerivativeFilter.html.

CMS

Wolfram Language. 2012. "PIDDerivativeFilter." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PIDDerivativeFilter.html.

✖
Wolfram Language. 2012. "PIDDerivativeFilter." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PIDDerivativeFilter.html.

APA

Wolfram Language. (2012). PIDDerivativeFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PIDDerivativeFilter.html

✖
Wolfram Language. (2012). PIDDerivativeFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PIDDerivativeFilter.html

BibTeX

@misc{reference.wolfram_2025_pidderivativefilter, author="Wolfram Research", title="{PIDDerivativeFilter}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/PIDDerivativeFilter.html}", note=[Accessed: 19-June-2025 ]}

✖
@misc{reference.wolfram_2025_pidderivativefilter, author="Wolfram Research", title="{PIDDerivativeFilter}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/PIDDerivativeFilter.html}", note=[Accessed: 19-June-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_pidderivativefilter, organization={Wolfram Research}, title={PIDDerivativeFilter}, year={2012}, url={https://reference.wolfram.com/language/ref/PIDDerivativeFilter.html}, note=[Accessed: 19-June-2025 ]}

✖
@online{reference.wolfram_2025_pidderivativefilter, organization={Wolfram Research}, title={PIDDerivativeFilter}, year={2012}, url={https://reference.wolfram.com/language/ref/PIDDerivativeFilter.html}, note=[Accessed: 19-June-2025 ]}