ParameterEstimator

ParameterEstimator

EstimatedDistributionとFindDistributionParametersのオプションで，使用する母数推定を指定する．

詳細

  • 使用可能な基本的設定値
  • "MaximumLikelihood"対数尤度関数を最大化する
    "MethodOfMoments"原点の周りのモーメントにマッチする
    "MethodOfCentralMoments"中心モーメントにマッチする
    "MethodOfCumulants"キュムラントにマッチする
    "MethodOfFactorialMoments"階乗モーメントにマッチする
  • 最尤法は対数尤度関数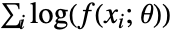を最大化する．ただし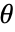， は分布母数で 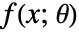は分布の確率密度関数である．
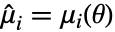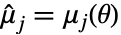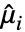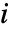
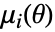  • モーメント法は , , を解く．ただし，は第 サンプルモーメントであり は母数が 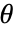の分布の第 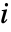モーメントである．
  • モーメント法には"MethodOfMoments"，"MethodOfCentralMoments"，"MethodOfCumulants"，"MethodOfFactorialMoments"がある．
  • ParameterEstimator->{mm, "MomentOrders"->list}とすると，list で指定されるモーメントの次数はモーメント法の推定器 mm によって使われる．
  • 一変量分布の場合，モーメントの次数は正の整数のリストでなければならない．
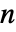  • 次元の分布の場合，モーメントの次数は長さ 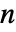で各リストの総和が正であるの非負の整数の複数のリストでなければならない．
  • ParameterEstimator->{"estimator",Method->"solver"}はもとになる方程式あるいは最適化ソルバのどれを使用するかを指定する．
  • "MaximumLikelihood"で使用可能なソルバ
  • Automatic自動的に選ばれたソルバ
    "FindMaximum"FindMaximumを使って対数尤度を最大化する
    "FindRoot"FindRootを使って尤度方程式を解く
    "NMaximize"NMaximizeを使って対数尤度を最大化する
  • "MethodOfMoments"，"MethodOfCentralMoments"，"MethodOfCumulants"，"MethodOfFactorialMoments"で使用可能なソルバ設定
  • Automatic自動的に選ばれたソルバ
    "FindRoot"FindRootを使ってモーメント方程式を解く
    "NSolve"NSolveを使ってモーメント方程式を解く
    "Solve"Solveを使ってモーメント方程式を解く
  • Automaticと設定すると，分布に基づいたソルバ（1つまたはいくつかのソルバの組合せ）と推定される母数が使われる．
  • ParameterEstimator->{"estimator",Method->{"solver",opts}}と設定すると，ソルバに追加オプションを与えることができる．
  • Solve，NSolve，NMaximizeのような初期値に依存しないソルバメソッドはEstimatedDistributionやFindDistributionParametersに与えられる初期値を利用しない．

例題

すべて開くすべて閉じる

例  (1)

最尤度母数推定を使って分布を構築する：

モーメント法に基づいた推定を使う：

2つの推定の密度間の差をプロットする：

スコープ  (4)

最尤度推定  (2)

デフォルトの方法を使って最尤度推定を得る：

NMaximizeを使って推定を得る：

デフォルトの方法を使って最尤度推定を得る：

FindMaximumとEvaluationMonitorを使ってサンプル点を抽出する：

サンプルとしての と の一連の値を可視化する：

モーメントに基づく推定  (2)

原点の周りのモーメントにマッチさせて母数を推定する：

他のモーメントに基づいた方法も一般に同様の値を与える：

デフォルトモーメントを使ったモーメント法で母数を推定する：

第1，第4モーメントを使う：

第2，第3階乗モーメントを使う：

特性と関係  (2)

FindDistributionParametersを使って最尤度推定を得る：

対数尤度を直接最大にして推定する：

FindDistributionParameters推定から最大化した値を計算する：

データのモーメント法推定を得る：

閉形式が存在する際にモーメントのマッチングで母数の値を求める：

記号解を得る：

データのモーメントを計算する：

データのモーメントを代入してモーメント法による推定を得る：

モーメント方程式を数値的に解く：

Wolfram Research (2010), ParameterEstimator, Wolfram言語関数， https://reference.wolfram.com/language/ref/ParameterEstimator.html.

テキスト

Wolfram Research (2010), ParameterEstimator, Wolfram言語関数， https://reference.wolfram.com/language/ref/ParameterEstimator.html.

CMS

Wolfram Language. 2010. "ParameterEstimator." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ParameterEstimator.html.

APA

Wolfram Language. (2010). ParameterEstimator. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ParameterEstimator.html

BibTeX

@misc{reference.wolfram_2024_parameterestimator, author="Wolfram Research", title="{ParameterEstimator}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/ParameterEstimator.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_parameterestimator, organization={Wolfram Research}, title={ParameterEstimator}, year={2010}, url={https://reference.wolfram.com/language/ref/ParameterEstimator.html}, note=[Accessed: 22-November-2024 ]}