WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

FindDistributionParameters
✖
FindDistributionParameters

✖

finds the parameter estimates for the distribution dist from data.

✖
FindDistributionParameters[data,dist,{{p,p0},{q,q0},…}]

finds the parameters p, q, … with starting values p0, q0, ….

Details and Options

  • FindDistributionParameters returns a list of replacement rules for the parameters in dist.
  • The data must be a list of possible outcomes from the given distribution dist.
  • The distribution dist can be any parametric univariate, multivariate, or derived distribution with unknown parameters.
  • The following options can be given:
  • AccuracyGoalAutomaticthe accuracy sought
    ParameterEstimator "MaximumLikelihood"what parameter estimator to use
    PrecisionGoalAutomaticthe precision sought
    WorkingPrecision Automaticthe precision used in internal computations
  • The following basic settings can be used for ParameterEstimator:
  • "MaximumLikelihood"maximize the log‐likelihood function
    "MethodOfMoments"match raw moments
    "MethodOfCentralMoments"match central moments
    "MethodOfCumulants"match cumulants
    "MethodOfFactorialMoments"match factorial moments
  • The maximum likelihood method attempts to maximize the log-likelihood function 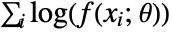, where 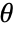are the distribution parameters and 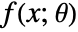is the PDF of the distribution.
  • The method of moments solves 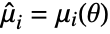, , 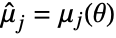where 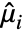is the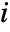 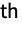^(th) sample moment and 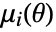is the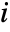 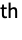^(th) moment of the distribution with parameters .
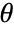  • Method-of-moment-based estimators may not satisfy all restrictions on parameters.

Examples

open allclose all

Basic Examples  (3)Summary of the most common use cases

Obtain the maximum likelihood parameter estimates assuming a Laplace distribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-fm0bw
Out[1]=1

Obtain the method of moments estimates:

In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-xr2lh
Out[2]=2

Estimate parameters for a multivariate distribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-blkneb
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-c7rr12
Out[2]=2

Compare the difference between the original and estimated PDFs:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-dqcr77
Out[3]=3

Estimate parameters from quantity data:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-fis4jx
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-2xwdq
Out[2]=2

Scope  (15)Survey of the scope of standard use cases

Basic Uses  (5)

Estimate both parameters for a binomial distribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-fo3xut
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-b5qgnt
Out[2]=2

Estimate p, assuming n is known:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-fjpgxw
Out[3]=3

Estimate n, assuming p is known:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-coeb7e
Out[4]=4

Get the distribution with maximum likelihood parameter estimate for a particular family:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-mkxzvl
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-xqjzb
Out[2]=2

Check goodness of fit by comparing a histogram of the data and the estimate's PDF:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-chdlxh
Out[3]=3

Perform goodness-of-fit tests with null distribution from res:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-h79ysd
Out[4]=4

Perform tests correcting for estimation of the parameter:

In[5]:=5
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-p8osoh
Out[5]=5

Estimate parameters by maximizing the log‐likelihood:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-cvbqgt
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-i7a7vi
Out[2]=2

Plot the log‐likelihood function to visually check that the solution is optimal:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-kudrs0
Out[3]=3

Visualize a log‐likelihood surface to find rough values for the parameters:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-hh5i95
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-e00bj2
Out[2]=2

Supply those rough values as starting values for the estimation:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-pk23z
Out[3]=3

Mark the optimal point on the contour plot:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-em6vw
Out[4]=4

Estimate the normal approximation of Poisson data:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-f1ubxc
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-bmydzo
Out[2]=2

Obtain estimate to 20 digits:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-hkaonz
Out[3]=3

Univariate Parametric Distributions  (2)

Estimate parameters for a continuous distribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-gkoovd
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ciirgu
Out[2]=2

Estimate parameters for a discrete distribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-0quwi
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-g86gb5
Out[2]=2

Compare the fitted and empirical CDFs:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-uw5ad
Out[3]=3

Multivariate Parametric Distributions  (2)

Estimate parameters for a discrete multivariate distribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-huw5eo
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ish72
Out[2]=2

Estimate parameters for a continuous multivariate distribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-dhbwo8
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-fx7s83
Out[2]=2

Visualize the density functions for the marginal distributions:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-iyla3o
Out[3]=3

Obtain the covariance matrix from the formula:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-bj72zx

Derived Distributions  (6)

Estimate parameters for a truncated normal:

In[5]:=5
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-cnhaze
In[7]:=7
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-b4it3n
Out[7]=7

Estimate parameters for a constructed distribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-xjacs
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-cz6xar
In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-d6iz7v
Out[3]=3

Visualize the optimal point:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-y463r
Out[4]=4

Estimate parameters for a product distribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ove1pe
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-iqkewk
Out[2]=2

Estimate parameters for a copula distribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-kajyvr
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-dmkw55
Out[2]=2

Estimate parameters for a component mixture:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-g5qjhs
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-mtt53t
In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-dsbx4n
Out[3]=3

Estimate the mixture probabilities assuming the component distributions are known:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-x5j0n
In[5]:=5
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-x4o55
Out[5]=5

Visualize the two estimates against the data:

In[6]:=6
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-h2saa9
Out[6]=6

Estimate parameters for a distribution in specified units:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-hs2lg0
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-g7ukc3
Out[2]=2

Options  (4)Common values & functionality for each option

ParameterEstimator  (3)

Estimate parameters by matching cumulants:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-g5q7z
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-llvug
Out[2]=2

Other moment‐based methods typically give similar results:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-r9j6s
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-mwobp
Out[4]=4

Estimate parameters based on default moments:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-i67wap
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-g9rzs0
Out[2]=2

Estimate parameters from the first and fourth moments:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-esvrcm
Out[3]=3

Obtain the maximum likelihood estimates using the default method:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-o6nc6
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-lvp1uu
Out[2]=2

Use FindMaximum to obtain the estimates:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-e9e0he
Out[3]=3

Use EvaluationMonitor to extract the points sampled:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-j6vhwp

Visualize the sequences of sampled and values:

In[5]:=5
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-bo0p03
Out[5]=5

WorkingPrecision  (1)

Use machine precision for continuous parameters by default:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-l1u6qi
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-8dyx1
Out[2]=2

Obtain a higher-precision result:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-rtyhv
Out[3]=3

Applications  (17)Sample problems that can be solved with this function

Use One Parameter Estimator to Get Starting Values for Another  (1)

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-f80lyr

Get the method of moments estimate:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ht4hfs
Out[1]=1

Use the method of moments estimate as the starting value for ml estimation:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-b04qb7
Out[1]=1

Obtain ml estimates for a gamma distribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-meun6x
Out[1]=1

Use those as starting values for the method of moments:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-d0jp9x
Out[1]=1

Obtain Starting Values for Another Estimation  (1)

Estimate Laplace parameters for data from an ExponentialPowerDistribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-hlweg
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-c8mi27
Out[2]=2

Use the Laplace estimate as a starting point for estimating exponential power parameters:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-bvt8i2
Out[3]=3

Compare the data with the Laplace and exponential power estimates:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-br232x
Out[4]=4

Parameter Estimation of Similarly Shaped Distributions  (1)

Model lognormal distributed data with a gamma distribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-fzzzxm
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-fg63nf
In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-jsaju
Out[3]=3

Compare the distributions of the simulation and estimated distributions:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-qormqv
Out[4]=4

Accident Claims  (1)

The number of accident claims per policy per year from an insurance company:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-z1vmig

Estimate the parameter for a logarithmic series distribution for policy claims shifted by 1:

In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-rcq9w9
Out[2]=2

See that the estimate gives a maximal result:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-cw79i2
Out[3]=3

Word Lengths in Different Languages  (1)

Get word length data for several languages:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-6iya5
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-eylvaw

Model the word lengths for each language as binomially distributed with :

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-dwvuty
Out[3]=3

Compare the actual and estimated distributions:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-nyixdm
Out[4]=4

Bootstrap the distribution of p values based on these 9 results:

In[5]:=5
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-cmv265
In[6]:=6
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-eupw67
Out[6]=6

Estimate the expected value of p and a standard deviation for the estimate:

In[7]:=7
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-h1zot0
Out[7]=7

Text Frequency  (1)

The word count in a text follows a Zipf distribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ir5i5j
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-z0k8fd

Fit a ZipfDistribution to the word frequency data:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-798qy3
Out[3]=3

Fit a truncated ZipfDistribution to counts at most 50 using rhohat as a starting value:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-hxqqsw
Out[4]=4

Visualize the CDFs up to the truncation value:

In[5]:=5
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-enj6pg
Out[5]=5

Estimate the proportion of the original data not included in the truncated model:

In[6]:=6
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-cxgs8z
Out[6]=6
In[7]:=7
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-lndm5
Out[7]=7

Earthquake Magnitudes  (1)

Find estimates for a multimodal MixtureDistribution model:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-edpm4u
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-f4t8ts

The magnitudes of earthquakes in the United States in the selected years have two modes:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-nxet3k
Out[3]=3

Fit distribution from possible mixtures of one NormalDistribution with another:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-i54v31
In[5]:=5
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-pk5e3b
Out[5]=5

Extract the means of the components:

In[6]:=6
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-by7qf7
Out[6]=6

The components' means are far enough apart that they are still the modes:

In[7]:=7
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-iwn8pm
Out[7]=7

Wind Speed Analysis  (1)

Model monthly maximum wind speeds in Boston:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-lwm8or

Fit the data to a RayleighDistribution:

In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-f4qsgb
Out[2]=2

An ExtremeValueDistribution:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-u25hr1
Out[3]=3

Compare the empirical and fitted quantiles to see where the models deviate from the data:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-6x1hxc
Out[4]=4

Distribution of Incomes  (1)

Model incomes at a large state university:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-7j991j
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-5shjys
In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-o5p1x5

Assume the salaries are Dagum distributed:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-5b4k5i
Out[4]=4

Assume they follow a more general Pareto distribution:

In[5]:=5
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-rpk1fh
Out[5]=5

Compare the subtle differences in the estimated distributions:

In[6]:=6
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-8iui9
Out[6]=6

Market Change in Stock Values  (1)

Use a beta distribution to model the proportion of Dow Jones Industrial stocks that increase in value on a given day:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-hhnw8h
Out[3]=3

Find daily change for Dow Jones Industrial stocks:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-c0r0j1

Number of days for each financial entity:

In[5]:=5
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-e15an6
Out[5]=5

Extract values from time series for each entity and normalize numeric quantities:

In[6]:=6
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-nob1rw

Check if each entity has the same length of data:

In[7]:=7
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ldtuwa
Out[7]=7
In[8]:=8
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-oibkmk
Out[8]=8

Calculate the daily ratio of companies with an increase in value:

In[9]:=9
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-b1xazx

Find parameter estimates, excluding days with zero or all companies having an increase in value:

In[10]:=10
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-18xqlp
Out[11]=11

Visualize the likelihood contours and mark the optimal point:

In[12]:=12
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-gxw5rz
Out[12]=12

Automobile Fuel Efficiency  (1)

The average city and highway mileage for midsize cars follows a binormal distribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-2zftgd

Assume city and highway miles per gallon are normally distributed and correlated:

In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-wivilb
Out[2]=2

Extract the estimated average city and highway mileages:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ejv7ci
Out[3]=3

Extract the estimated correlation between city and highway mileages:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-219ou
Out[4]=4

Visualize the joint density on a logarithmic scale with the mean mileage marked with a blue point:

In[5]:=5
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-mvwyjp
Out[5]=5

Earthquake Waiting Times  (1)

The data contains waiting times in days between serious (magnitude at least 7.5 or over 1000 fatalities) earthquakes worldwide, recorded from 12/16/1902 to 3/4/1977:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-nreqgi

Model waiting times by an ExponentialDistribution:

In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-junv9u
Out[2]=2

Estimate the average and median number of days between major earthquakes:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-xmtz1i
Out[3]=3

Earthquake Frequency  (1)

The number of earthquakes per year can be modeled by SinghMaddalaDistribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ksja6c
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ehjcp4
Out[2]=2

Fit the distribution to the data:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-bk6atw
Out[3]=3

Compute the maximized log‐likelihood:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-cfviox
Out[4]=4

Visualize the log‐likelihood profiles near the optimal parameter values:

In[5]:=5
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-c4s2w3
Out[5]=5

Time between Geyser Eruptions  (1)

Mixtures can be used to model multimodal data:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-wffeo8
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-jtc6yw

A histogram of waiting times for eruptions of the Old Faithful geyser exhibits two modes:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-56feeh
Out[3]=3

Fit a mixture of gamma and normal distributions to the data:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-08arub
In[5]:=5
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-h1dwv5
Out[5]=5

Compare the histogram to the PDF of the estimated distribution:

In[6]:=6
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-8eqwhv
Out[6]=6

Stock Price Distribution  (1)

Lognormal distribution can be used to model stock prices:

In[9]:=9
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-1vd54a

Fit the distribution to the data:

In[10]:=10
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-t4z02a
Out[10]=10

Visualize the profile likelihoods, fixing one parameter at the fitted value:

In[18]:=18
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ge95q4
Out[18]=18

Water Flow Rates  (1)

Consider the annual minimum daily flows given in cubic meters per second for the Mahanadi river:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-9jny36

Model the annual minimum mean daily flows as a MinStableDistribution:

In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-9l18qo
Out[2]=2

Simulate annual minimum mean daily flows for the next 30 years:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-o3eth1
Out[3]=3

Population Sizes  (1)

Use a Pareto distribution to model Australian city population sizes:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-mv1s6f
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-45n2wx
In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-qmih4s
Out[3]=3

Get the probability that a city has a population at least 10000 under a Pareto distribution:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-f2ken6
Out[4]=4

Compute the probability given the parameter estimates:

In[5]:=5
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-djigbb
Out[5]=5

Compute the probability based on the original data:

In[6]:=6
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ddnga0
Out[6]=6

Properties & Relations  (8)Properties of the function, and connections to other functions

FindDistributionParameters gives estimates as replacement rules:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-e3jtwd
Out[1]=1

EstimatedDistribution gives a distribution with parameter estimates inserted:

In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-e4ishy
Out[2]=2

FindProcessParameters returns a list of parameter estimates for a random process:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-fa9tm0
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-wtkc3
Out[2]=2

FindDistributionParameters returns a list of parameter estimates for a distribution:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-1dde8
In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-yq9vm
Out[4]=4

Estimate distribution parameters by maximum likelihood:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ob999
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-lczwnz
Out[2]=2

Use DistributionFitTest to test quality of the fit:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ccvtx8
Out[3]=3

Extract the fitted distribution parameter:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-h761n
Out[4]=4

Obtain a table of relevant test statistics and p‐values:

In[5]:=5
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ihsqf
Out[5]=5

Estimate parameters in a parametric distribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ckutmu
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-isciqb
Out[2]=2

Get a nonparametric kernel density estimate using SmoothKernelDistribution:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-7599f
Out[3]=3

Compare the PDFs for the nonparametric and parametric distributions:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-do791o
Out[4]=4

Visualize the nonparametric density using SmoothHistogram:

In[5]:=5
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-dx56th
Out[5]=5

Get a maximum likelihood estimate of parameters:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-b44vfh
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-gybs4p
Out[2]=2

Compute the likelihood using Likelihood:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-d6khwy
Out[3]=3

Compute the log‐likelihood using LogLikelihood:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ee9gr
Out[4]=4

Estimate parameters by matching raw moments:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-j6kgfw
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-c76r62
Out[2]=2

Compute raw moments from the data using Moment:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-bfhulb
Out[3]=3

Compute the same moments from the beta distribution for the estimated parameters:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-b4c4k2
Out[4]=4

Estimate parameters for a Weibull distribution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-k52now
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-b1yhwi
Out[2]=2

Use QuantilePlot to visualize the empirical quantiles versus the theoretical quantiles:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-jlzx1q
Out[3]=3

Obtain the same visualization when the estimation is done within QuantilePlot:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-e6tfs7
Out[4]=4

FindDistributionParameters ignores time stamps in TimeSeries and EventSeries:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-5cnypl
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-to38xt
Out[2]=2

The same as:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-d86q20
Out[3]=3

For TemporalData, all the path structure is ignored:

In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ldkb7z
In[5]:=5
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-h4n01u
Out[5]=5

The same as:

In[6]:=6
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-o8g3s9
Out[6]=6

Possible Issues  (3)Common pitfalls and unexpected behavior

Solutions of method-of-moment equations can give parameters that are not valid:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-cez6ga
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-6tf1w
Out[2]=2

For a continuous distribution:

In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-vi8it0
In[4]:=4
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-j8q9s
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-4ii0py
Out[5]=5

Good starting values may be needed to obtain a good solution:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-d6zcjm
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-rshcwr
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-ehtcct
Out[3]=3

Good starting values may result in quicker results:

In[1]:=1
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-haflfw
In[2]:=2
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-exmjzn
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0elts4n1fh6o5lv-81orm
Out[3]=3
Wolfram Research (2010), FindDistributionParameters, Wolfram Language function, https://reference.wolfram.com/language/ref/FindDistributionParameters.html.
✖
Wolfram Research (2010), FindDistributionParameters, Wolfram Language function, https://reference.wolfram.com/language/ref/FindDistributionParameters.html.

Text

Wolfram Research (2010), FindDistributionParameters, Wolfram Language function, https://reference.wolfram.com/language/ref/FindDistributionParameters.html.

✖
Wolfram Research (2010), FindDistributionParameters, Wolfram Language function, https://reference.wolfram.com/language/ref/FindDistributionParameters.html.

CMS

Wolfram Language. 2010. "FindDistributionParameters." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FindDistributionParameters.html.

✖
Wolfram Language. 2010. "FindDistributionParameters." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FindDistributionParameters.html.

APA

Wolfram Language. (2010). FindDistributionParameters. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindDistributionParameters.html

✖
Wolfram Language. (2010). FindDistributionParameters. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindDistributionParameters.html

BibTeX

@misc{reference.wolfram_2025_finddistributionparameters, author="Wolfram Research", title="{FindDistributionParameters}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/FindDistributionParameters.html}", note=[Accessed: 29-March-2025 ]}

✖
@misc{reference.wolfram_2025_finddistributionparameters, author="Wolfram Research", title="{FindDistributionParameters}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/FindDistributionParameters.html}", note=[Accessed: 29-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_finddistributionparameters, organization={Wolfram Research}, title={FindDistributionParameters}, year={2010}, url={https://reference.wolfram.com/language/ref/FindDistributionParameters.html}, note=[Accessed: 29-March-2025 ]}

✖
@online{reference.wolfram_2025_finddistributionparameters, organization={Wolfram Research}, title={FindDistributionParameters}, year={2010}, url={https://reference.wolfram.com/language/ref/FindDistributionParameters.html}, note=[Accessed: 29-March-2025 ]}