ParameterEstimator
是 EstimatedDistribution 和 FindDistributionParameters 的一个选项,指定要使用什么参数估计方法.
更多信息



- 可以使用以下基本设置:
-
"MaximumLikelihood" 最大化对数似然函数 "MethodOfMoments" 匹配原始矩 "MethodOfCentralMoments" 匹配中心矩 "MethodOfCumulants" 匹配累积量 "MethodOfFactorialMoments" 匹配阶乘矩 - 最大似然方法将最大化对数似然函数
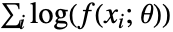 ,其中
,其中 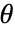 是分布参数,
是分布参数,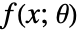 是分布的概率密度函数.
是分布的概率密度函数. - 矩量法求解
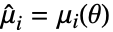 、
、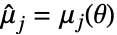 、
、 其中
其中 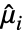 是第
是第 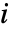
 阶样本矩,而
阶样本矩,而 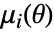 是参数为
是参数为 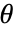 的分布的第
的分布的第 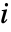 阶矩.
阶矩. - 不同矩量法包括:"MethodOfMoments"、"MethodOfCentralMoments"、"MethodOfCumulants" 或者 "MethodOfFactorialMoments".
- 在 ParameterEstimator->{mm, "MomentOrders"->list} 下,由 list 指定的矩的阶数用于矩估计 mm 方法.
- 对于单变量分布,矩的阶数应该是由正整数组成的列表.
- 对于
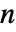 维分布,矩的阶数应该是由非负整数组成的长度为
维分布,矩的阶数应该是由非负整数组成的长度为 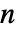 的列表,其中每个列表的和为一个正整数.
的列表,其中每个列表的和为一个正整数. - ParameterEstimator->{"estimator",Method->"solver"} 指定要使用的内部方程或者优化求解器.
- "MaximumLikelihood" 的可能求解器设置包括:
-
Automatic 自动选择的求解器 "FindMaximum" 使用 FindMaximum 最大化对数似然函数 "FindRoot" 使用 FindRoot 求解似然方程 "NMaximize" 使用 NMaximize 最大化对数似然函数 - "MethodOfMoments"、"MethodOfCentralMoments"、"MethodOfCumulants" 和"MethodOfFactorialMoments" 的可能求解器设置包括:
-
Automatic 自动选择的求解器 "FindRoot" 使用 FindRoot 求解矩方程 "NSolve" 使用 NSolve 求解矩方程 "Solve" 使用 Solve 求解矩方程 - Automatic 设置基于分布和要估计的参数,使用一个求解器或者求解器组合.
- 在设置 ParameterEstimator->{"estimator",Method->{"solver",opts}} 下,可以对求解器给出额外的选项.
- 依赖于初始值的求解方法,如 Solve、NSolve 和 NMaximize 将不使用对 EstimatedDistribution 或者FindDistributionParameters 给出的初始值.
范例
打开所有单元关闭所有单元范围 (4)
最大似然估计值 (2)
使用 NMaximize 获得估计值:
使用 FindMaximum 和 EvaluationMonitor 提取样本点:
属性和关系 (2)
使用 FindDistributionParameters 获得最大似然估计值:
从 FindDistributionParameters 估计中计算最大值:
Wolfram Research (2010),ParameterEstimator,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ParameterEstimator.html.
文本
Wolfram Research (2010),ParameterEstimator,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ParameterEstimator.html.
CMS
Wolfram 语言. 2010. "ParameterEstimator." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ParameterEstimator.html.
APA
Wolfram 语言. (2010). ParameterEstimator. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ParameterEstimator.html 年