Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Pi

表示，其数值 .

更多信息

数学常量，NumericQ 视为数值，D 视为常量.
Pi 可以通过 N 计算到任意数值精度.
Pi 可以在 StandardForm 和 InputForm 中以 π、pi、p 或 \[Pi]输入.
在 StandardForm 中，Pi 输出 π.

背景

Pi 是表示数学常数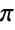的符号，可用 ∖[Pi] 输入. Pi 被定义为圆的周长和直径的比值，数值 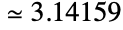. Pi 广泛出现在许多数学计算中，包括三角学表达式、特殊函数值、求和、求积、积分以及其它数学和科学领域的诸多公式.
当 Pi 作为符号时，它被当成精确值参与计算. 尽管许多含有 Pi 的表达式（例如 Cos[Pi/10]）会自动展开成由简单函数组成的项，但展开及化简一些更复杂的含有 Pi 的表达式（例如 Cos[Pi/15]）还是需要用到如 FunctionExpand 和 FullSimplify 这样的函数.
Pi 既是无理数也是超越数，这意味着它既不能被表示成整数的比值也不是任何整数系数多项式的根. 虽然现在还不知道 Pi 是否是某个进位制下的正规数（这意味着它在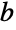进制下的各位数字均匀分布），但它的各位数字分布得非常均匀.
用 N 可以根据楚德诺夫斯基公式算出 Pi 的任意精度的数值. 事实上在一台现代台式电脑上计算 Pi 的前一百万位数字耗时都不到一秒. RealDigits 可用于返回 Pi 的各位数字列表而 ContinuedFraction 则可得到其连分数展开的各项.
Wolfram 语言中许多与角度相关的函数都以弧度值作为变量并返回弧度值的结果. 因此实际上等于 Pi/180 的符号 Degree 可在需要使用角度值的时候作为乘数（例如 Cos[30 Degree]）.

范例

打开所有单元关闭所有单元

基本范例 (3)

Pi 可以用 p 来输入：

计算到任意精度：

执行一个精确数值计算：

范围 (1)

以 10 为底的的第一百万位数字：

应用 (5)

求一个圆的面积：

以 10 为底的的前 20 个数字：

具有以弧度为单位的自变量的三角函数：

许多数学函数和运算给出关于 π 的结果：

属性和关系 (2)

自动使用各种符号关联：

Pi 在微分中视为常量：

巧妙范例 (2)

对于的二进制数字的随机行走：

连分数的项：

顶部