Some Mathematical Functions
Some Mathematical Functions
The Wolfram Language includes a very large collection of mathematical functions. "Mathematical Functions" gives the complete list. Here are a few of the common ones.
| Sqrt[x] |
square root (
|
| Exp[x] |
exponential (
|
| Log[x] |
natural logarithm (
|
| Log[b,x] | logarithm to base |
| Sin[x],Cos[x],Tan[x] |
trigonometric functions (with arguments in radians)
|
| ArcSin[x],ArcCos[x],ArcTan[x] | inverse trigonometric functions |
| n! |
factorial (product of integers
|
| Abs[x] | absolute value |
| Round[x] | closest integer to |
| Mod[n,m] | |
| RandomReal[] | pseudorandom number between 0 and 1 |
| Max[x,y,…],Min[x,y,…] |
maximum, minimum of
|
| FactorInteger[n] |
■ The arguments of all Wolfram Language functions are enclosed in square brackets. |
■ The names of built‐in Wolfram Language functions begin with capital letters. |
It is important to remember that all function arguments in the Wolfram Language are enclosed in square brackets, not parentheses. Parentheses in the Wolfram Language are used only to indicate the grouping of terms, and never to give function arguments.
Just as with arithmetic operations, the Wolfram Language tries to give exact values for mathematical functions when you give it exact input.
The presence of an explicit decimal point tells the Wolfram Language to give an approximate numerical result:
Since you are not asking for an approximate numerical result, the Wolfram Language leaves the number here in an exact symbolic form:
Here is the exact integer result for 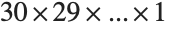 . Computing factorials like this can give you very large numbers. You should be able to calculate up to at least 2000! in a short time:
. Computing factorials like this can give you very large numbers. You should be able to calculate up to at least 2000! in a short time:
| Pi | |
| E | |
| Degree | |
| I | |
| Infinity |
This gives the exact result for  . Notice that the arguments to trigonometric functions are always in radians:
. Notice that the arguments to trigonometric functions are always in radians:
This gives the numerical value of  . Multiplying by the constant Degree converts the argument to radians:
. Multiplying by the constant Degree converts the argument to radians:
You can get logarithms in any base b using Log[b,x]. As in standard mathematical notation, the b is optional: