PlanckRadiationLaw

PlanckRadiationLaw[temperature,λ]

返回指定温度和波长 λ 的光谱辐射率.

PlanckRadiationLaw[temperature,f]

返回指定温度和频率 f 的光谱辐射率.

PlanckRadiationLaw[temperature,property]

返回光谱辐射率与波长的关系图.

PlanckRadiationLaw[temperature,{λ1,λ2}]

返回光谱辐射率在 λ1 到 λ2 的波长范围内的积分.

PlanckRadiationLaw[temperature,{f1,f2}]

返回光谱辐射率在 f1 到 f2 的频率范围内的积分.

更多信息

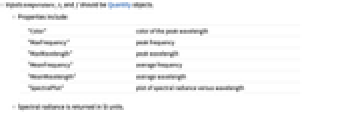
  • 输入 temperature、λ 和 f 必须是 Quantity 对象.
  • 属性包括：
  • "Color"峰值波长的颜色
    "MaxFrequency"峰值频率
    "MaxWavelength"峰值波长
    "MeanFrequency"平均频率y
    "MeanWavelength"平均波长
    "SpectralPlot"光谱辐射率 vs 波长图
  • 返回光谱辐射率的单位为 SI 单位.

范例

打开所有单元关闭所有单元

基本范例  (2)

求光谱辐射率：

由频率确定光谱辐射率：

察看 Quantity[300,"DegreesCelsius"] 的光谱辐射率的形状：

求平均波长：

求峰值波长的颜色：

范围  (3)

查看 PlanckRadiationLaw 的所有属性：

求 6000 K 时的峰值波长和颜色：

确定 6000 K 时的峰值频率：

求光谱辐射亮度在波长或频率范围上的积分：

应用  (5)

计算作为波长的函数时，最大辐射率对应的波长：

计算作为频率的函数时，最大辐射率对应的频率：

请注意该峰值并不对应于同一个波长：

察看光谱辐射率随频率变化的情况：

用方向性温度（考虑相对论效应并校正）来观察一个以相对论速度移动的物体，研究其光谱辐射率的峰值怎样向长波长偏移：

演示维恩位移定律, 峰值波长与自身温度之间成反比关系的定律：

通过对光谱的主要部分积分并使用兰伯特余弦定律推导出黑体表面上的点的角因子，通过近似普朗克定律的积分来找到辐射出射度：

除以温度的四次方求 Stefan–Boltzmann 常数：

属性和关系  (1)

PlanckRadiationLaw 使用的公式和在 FormulaData 中出现的公式是一样的：

巧妙范例  (2)

比较普朗克辐射定律和维恩分布定律：

比较维恩分布定律、瑞利-金斯定律以及普朗克辐射定律：

在微米级大小的盒子中，量子效应使得可能的最小的频率为：

考虑在无限大腔体中的黑体的有限尺寸效应，绘制盒内的能量密度：

Wolfram Research (2014)，PlanckRadiationLaw，Wolfram 语言函数，https://reference.wolfram.com/language/ref/PlanckRadiationLaw.html （更新于 2016 年）.

文本

Wolfram Research (2014)，PlanckRadiationLaw，Wolfram 语言函数，https://reference.wolfram.com/language/ref/PlanckRadiationLaw.html （更新于 2016 年）.

CMS

Wolfram 语言. 2014. "PlanckRadiationLaw." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/PlanckRadiationLaw.html.

APA

Wolfram 语言. (2014). PlanckRadiationLaw. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/PlanckRadiationLaw.html 年

BibTeX

@misc{reference.wolfram_2024_planckradiationlaw, author="Wolfram Research", title="{PlanckRadiationLaw}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/PlanckRadiationLaw.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_planckradiationlaw, organization={Wolfram Research}, title={PlanckRadiationLaw}, year={2016}, url={https://reference.wolfram.com/language/ref/PlanckRadiationLaw.html}, note=[Accessed: 22-November-2024 ]}