PoissonPDEComponent
PoissonPDEComponent[vars,pars]
ポアソン(Poisson)PDE項 ![]() をモデル変数 vars,モデルパラメータ pars で与える.
をモデル変数 vars,モデルパラメータ pars で与える.
詳細


- PoissonPDEComponentは,偏微分方程式で使う微分演算子の和を返す.
- PoissonPDEComponentを使って,従属変数
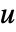 ,独立変数
,独立変数 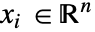 ,時間変数
,時間変数 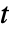 でポアソン方程式をモデル化することができる.
でポアソン方程式をモデル化することができる. - 定常モデル変数 vars は vars={u[x1,…,xn],{x1,…,xn}}である.
- 時間依存モデル変数 vars は vars={u[t,x1,…,xn],t,{x1,…,xn}}である.
- PoissonPDEComponentは拡散とソース項に基づいている.
- 拡散係数–1を持つポアソンPDE項
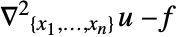 はDiffusionPDETermとして実現され,係数
はDiffusionPDETermとして実現され,係数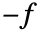 を持つSourcePDETermは結果として
を持つSourcePDETermは結果として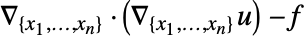 になる,
になる, - 次のモデルパラメータ pars を与えることができる.
-
パラメータ デフォルト シンボル "PoissonSourceTerm" 1 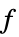
"RegionSymmetry" None 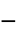
- ソース項の係数
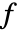 はスカラーである.
はスカラーである. - ソース項の係数
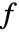 は,時間,空間,パラメータ,従属変数に依存することができる.
は,時間,空間,パラメータ,従属変数に依存することができる. - パラメータ"RegionSymmetry"の可能な選択肢には"Axisymmetric"がある.
- "Axisymmetric"領域対称性は,角変数を以下のように削除することで円筒座標が削減された切頂円筒座標系を表す.
-
次元 削減 方程式 1D 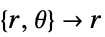
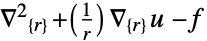
2D 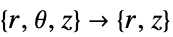
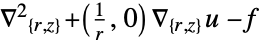
- 拡散係数1はNeumannValueの意味に影響する.
- PoissonPDEComponentが連想 pars で…,keypi…,pivi,…]として指定されるパラメータ
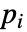 に依存するなら,パラメータ
に依存するなら,パラメータ 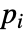 は
は 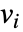 で置換される.
で置換される.
例題
すべて開くすべて閉じるアプリケーション (1)
中実円柱内の軸対称ポアソン問題を解く.変数とパラメータを定義する:
中実円柱は立体の断面を表す2Dの長方形で近似できる.Polygonを使って2Dの長方形を作成する:
DensityPlotで解を可視化する:
Wolfram Research (2020), PoissonPDEComponent, Wolfram言語関数, https://reference.wolfram.com/language/ref/PoissonPDEComponent.html (2022年に更新).
テキスト
Wolfram Research (2020), PoissonPDEComponent, Wolfram言語関数, https://reference.wolfram.com/language/ref/PoissonPDEComponent.html (2022年に更新).
CMS
Wolfram Language. 2020. "PoissonPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/PoissonPDEComponent.html.
APA
Wolfram Language. (2020). PoissonPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PoissonPDEComponent.html