PoissonPDEComponent
PoissonPDEComponent[vars,pars]
生成泊松 PDF 项 ![]() ,其中模型变量为 vars,模型参数为 pars.
,其中模型变量为 vars,模型参数为 pars.
更多信息


- PoissonPDEComponent 返回微分算子的总和,以用作偏微分方程的一部分:
- PoissonPDEComponent 可用于模拟泊松方程,其中因变量为
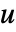 ,自变量为
,自变量为 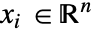 和时间变量为
和时间变量为 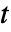 .
. - 平稳模型变量 vars 为 vars={u[x1,…,xn],{x1,…,xn}}.
- 与时间相关的模型变量 vars 为 vars={u[t,x1,…,xn],t,{x1,…,xn}}.
- PoissonPDEComponent 基于扩散项和源项:
- 泊松 PDF 项
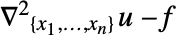 被实现为扩散系数为 –1 的 DiffusionPDETerm 和系数为
被实现为扩散系数为 –1 的 DiffusionPDETerm 和系数为 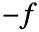 的 SourcePDETerm,得到
的 SourcePDETerm,得到 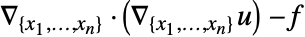 .
. - 可以给出以下模型参数 pars:
-
参数 缺省值 符号 "PoissonSourceTerm" 1 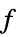
"RegionSymmetry" None 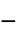
- 源项系数
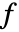 是标量.
是标量. - 源项系数
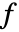 可以取决于时间、空间、参数和因变量.
可以取决于时间、空间、参数和因变量. - 参数 "RegionSymmetry" 的一个可能选择是 "Axisymmetric".
- "Axisymmetric" 区域对称性代表了一个截断的圆柱坐标系,其中圆柱坐标通过移除角度变量进行化简,如下所示:
-
维数 化简 方程 1D 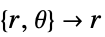
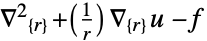
2D 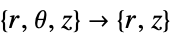
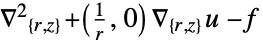
- 扩散系数 1 会影响 NeumannValue 的含义.
- 如果 PoissonPDEComponent 取决于参数
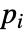 ,这些参数在关联解析 pars 中被指定为 …,keypi…,pivi,…,参数
,这些参数在关联解析 pars 中被指定为 …,keypi…,pivi,…,参数 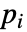 被替换成
被替换成 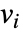 .
.
范例
打开所有单元关闭所有单元应用 (1)
实体圆柱体可以用一个代表实体横截面的二维矩形来近似. 使用 Polygon 创建二维矩形:
使用 DensityPlot 可视化求出的解:
Wolfram Research (2020),PoissonPDEComponent,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PoissonPDEComponent.html (更新于 2022 年).
文本
Wolfram Research (2020),PoissonPDEComponent,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PoissonPDEComponent.html (更新于 2022 年).
CMS
Wolfram 语言. 2020. "PoissonPDEComponent." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2022. https://reference.wolfram.com/language/ref/PoissonPDEComponent.html.
APA
Wolfram 语言. (2020). PoissonPDEComponent. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/PoissonPDEComponent.html 年