PrimePi
PrimePi[x]
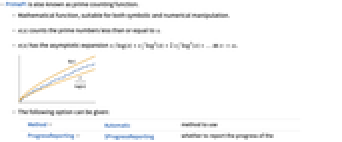
给出小于等于 x 的素数 ![]() 的数目.
的数目.
更多信息和选项
- PrimePi 也称为素数计数函数.
- 数学函数,适用于符号和数字运算.
![TemplateBox[{x}, PrimePi] TemplateBox[{x}, PrimePi]](Files/PrimePi.zh/2.png) 计算小于或等于 x 的素数的个数.
计算小于或等于 x 的素数的个数.- 当
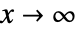 时,
时,![TemplateBox[{x}, PrimePi] TemplateBox[{x}, PrimePi]](Files/PrimePi.zh/4.png) 的渐进展开为
的渐进展开为 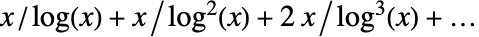 .
. - 可以给出以下选项:
-
Method Automatic 所用方法 ProgressReporting $ProgressReporting 是否报告计算进度 - Method 的可能设置包括:
-
"DelegliseRivat" 使用 Deléglise–Rivat 算法 "Legendre" 使用勒让德公式 "Lehmer" 使用 Lehmer 公式 "LMO" 使用 Lagarias–Miller–Odlyzko 算法 "Meissel" 使用 Meissel 公式 "Sieve" 使用埃拉托斯特尼筛法
范例
打开所有单元关闭所有单元
Wolfram Research (1991),PrimePi,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PrimePi.html (更新于 2021 年).
文本
Wolfram Research (1991),PrimePi,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PrimePi.html (更新于 2021 年).
CMS
Wolfram 语言. 1991. "PrimePi." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2021. https://reference.wolfram.com/language/ref/PrimePi.html.
APA
Wolfram 语言. (1991). PrimePi. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/PrimePi.html 年
