ZetaZero

ZetaZero[k]

represents the k^(th) zero of the Riemann zeta function on the critical line.

ZetaZero[k,t]

represents the k^(th) zero with imaginary part greater than t.

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • For positive k, ZetaZero[k] represents the zero of 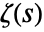on the critical line 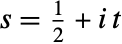that has the k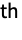^(th) smallest positive imaginary part.
  • For negative k, ZetaZero[k] represents zeros with progressively larger negative imaginary parts.
  • N[ZetaZero[k]] gives a numerical approximation to the specified zero.
  • ZetaZero can be evaluated to arbitrary numerical precision.
  • ZetaZero automatically threads over lists.

Examples

open allclose all

Basic Examples  (3)

Find numerically the position of the first zero:

Symbolic property:

Display zeros of the Im[Zeta[1/2+z]] function:

Scope  (8)

Numerical Evaluation  (3)

Evaluate numerically:

Evaluate to high precision:

Evaluate efficiently at high precision:

Specific Values  (3)

The first three zeros:

Find the first zero of Zeta[1/2+ x] using FindRoot:

ZetaZero threads elementwise over lists:

Visualization  (2)

Display zeros of Im[Zeta[1/2+ z]] function:

Show the first zero greater than 15:

Generalizations & Extensions  (1)

Negative order is interpreted as a reflected root of the Zeta function:

Applications  (5)

Plot distances between successive zeros:

Visualize the first 10 zeros:

Compute Gram points:

Show good Gram points, where RiemannSiegelZ changes sign for consecutive points:

Show a bad Gram point:

First occurrence of Lehmer's phenomenon:

Plot an approximation of the number of primes and prime powers using MangoldtLambda and ZetaZero:

The more zeros used, the closer the approximation:

Properties & Relations  (1)

Possible Issues  (1)

ZetaZero[0] is not defined:

Wolfram Research (2007), ZetaZero, Wolfram Language function, https://reference.wolfram.com/language/ref/ZetaZero.html.

Text

Wolfram Research (2007), ZetaZero, Wolfram Language function, https://reference.wolfram.com/language/ref/ZetaZero.html.

CMS

Wolfram Language. 2007. "ZetaZero." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ZetaZero.html.

APA

Wolfram Language. (2007). ZetaZero. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ZetaZero.html

BibTeX

@misc{reference.wolfram_2025_zetazero, author="Wolfram Research", title="{ZetaZero}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/ZetaZero.html}", note=[Accessed: 20-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_zetazero, organization={Wolfram Research}, title={ZetaZero}, year={2007}, url={https://reference.wolfram.com/language/ref/ZetaZero.html}, note=[Accessed: 20-February-2025 ]}