ReactionPDETerm[vars,a]
反応係数 ![]() ,モデル変数 vars の反応項
,モデル変数 vars の反応項 ![]() を表す.
を表す.
ReactionPDETerm[{u,{x1,…,xn}},a,pars]
モデルパラメータ pars を使う.


ReactionPDETerm
ReactionPDETerm[vars,a]
反応係数 ![]() ,モデル変数 vars の反応項
,モデル変数 vars の反応項 ![]() を表す.
を表す.
ReactionPDETerm[{u,{x1,…,xn}},a,pars]
モデルパラメータ pars を使う.
詳細


- 反応項は,生物学,化学,物理学等の数多くの分野で吸収や放出をモデル化するために使われている.
- 反応係数
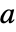 がある反応は,従属変数
がある反応は,従属変数 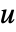 の吸収過程である.
の吸収過程である. - ReactionPDETermは,偏微分方程式の一部として使われる微分演算子項を返す.
- ReactionPDETermを使って,従属変数
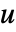 ,独立変数
,独立変数 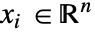 ,時間変数
,時間変数 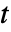 の反応方程式がモデル化できる.
の反応方程式がモデル化できる. - 定常モデル変数 vars は vars={u[x1,…,xn],{x1,…,xn}}である.
- 時間依存モデル変数 vars は vars={u[t,x1,…,xn],{x1,…,xn}}または vars={u[t,x1,…,xn],t,{x1,…,xn}}である.
- 他のPDE項との関連における反応項
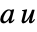 は以下で与えられる.
は以下で与えられる. - 反応係数
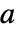 は次の形を持つことができる.
は次の形を持つことができる. -
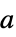
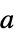
スカラー a - 従属変数が{u1,…,um}の偏微分方程式系についての反応は以下を表す.
- 次は,PDE項の系との関連における反応項である.
- 反応係数
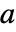 は
は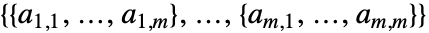 の形の階数2のテンソルである.各部分行列
の形の階数2のテンソルである.各部分行列 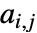 は単一の従属変数と同じ方法で指定できるスカラーである.
は単一の従属変数と同じ方法で指定できるスカラーである. - 反応係数
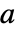 は,時間,空間,パラメータ,従属変数に依存することがある.
は,時間,空間,パラメータ,従属変数に依存することがある. - 係数
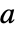 はNeumannValueの意味をもたらしはしない.
はNeumannValueの意味をもたらしはしない. - 独立変数に明示的には従属しないすべての数量の偏導関数は0であるとみなされる.
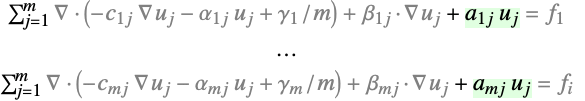
例題
すべて開く すべて閉じる関連するガイド
-
▪
- 偏微分方程式項
テキスト
Wolfram Research (2020), ReactionPDETerm, Wolfram言語関数, https://reference.wolfram.com/language/ref/ReactionPDETerm.html.
CMS
Wolfram Language. 2020. "ReactionPDETerm." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ReactionPDETerm.html.
APA
Wolfram Language. (2020). ReactionPDETerm. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ReactionPDETerm.html
BibTeX
@misc{reference.wolfram_2025_reactionpdeterm, author="Wolfram Research", title="{ReactionPDETerm}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/ReactionPDETerm.html}", note=[Accessed: 20-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_reactionpdeterm, organization={Wolfram Research}, title={ReactionPDETerm}, year={2020}, url={https://reference.wolfram.com/language/ref/ReactionPDETerm.html}, note=[Accessed: 20-February-2026]}