RenewalProcess
RenewalProcess[rdist]
到着間隔が rdist に従って分布する更新過程を表す.
詳細
- RenewalProcessは連続時間あるいは離散時間の離散状態過程である.
- RenewalProcessは rdist によって,離散状態・連続時間あるいは離散状態・離散時間のいずれかの過程である.
- 状態
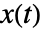 は0から
は0から 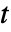 までの区間の事象数であり
までの区間の事象数であり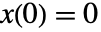 である.
である. - 分布 dist は正の領域にある任意の連続分布あるいは離散分布でよい.
- RenewalProcessは,Mean,PDF,Probability,RandomFunction等の関数で使うことができる.
例題
すべて開くすべて閉じるスコープ (6)
連続到着間隔分布 (2)
離散到着間隔分布 (2)
アプリケーション (1)
特性と関係 (2)
Wolfram Research (2012), RenewalProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/RenewalProcess.html.
テキスト
Wolfram Research (2012), RenewalProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/RenewalProcess.html.
CMS
Wolfram Language. 2012. "RenewalProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RenewalProcess.html.
APA
Wolfram Language. (2012). RenewalProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RenewalProcess.html