CompoundRenewalProcess

CompoundRenewalProcess[rdist,jdist]

represents a compound renewal process with renewal-time distribution rdist and jump size distribution jdist.

Details

  • CompoundRenewalProcess is also known as a renewal-reward process or cumulative renewal process.
  • CompoundRenewalProcess is a continuous-time process with continuous rdist, a discrete-time process for a discrete rdist, a continuous-state process with continuous jdist, and a discrete-state process with discrete jdist.
  • The distribution rdist can be any univariate distribution with non-negative domain. The distribution jdist can be any univariate distribution.
  • The state at time 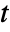is given by 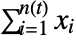, where the 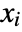are independent and identically distributed random variables following jdist and 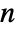follows RenewalProcess[rdist].
  • CompoundRenewalProcess can be used with such functions as Mean, Variance, and RandomFunction.

Examples

open allclose all

Basic Examples  (1)

Simulate a compound renewal process with gamma renewal times and exponential jumps:

Scope  (3)

Simulate a compound renewal process with discrete jumps:

Simulate a compound renewal process with continuous jumps:

Process parameters estimation:

Estimate the distribution parameters from sample data:

Applications  (2)

The hourly arrival of shoppers at a newly renovated store follows an Erlang distribution with shape parameter 2 and rate parameter 30. The store promotes this event by giving every customer a gift. The gift has a value that follows a WeibullDistribution with shape parameter 14 and scale parameter 3. Simulate the cost of the gift process during the 12-hour period for which the store is open that day and find the expected total cost to the store:

Simulate the process for 12 hours:

Expected total cost of the gifts given on the inaugural day:

Simulate the distribution of the cost:

Empirical probability density function:

Empirical probability that the store spends between $450 and $600 on the gifts:

Define a random walk process with steps following NormalDistribution:

Simulate:

Mean function:

Properties & Relations  (3)

CompoundRenewalProcess is a jump process:

Compound renewal process is not weakly stationary:

BinomialProcess is a special case of a compound renewal process:

The mean functions agree:

Create empirical covariance functions:

Compare the covariance functions:

Wolfram Research (2012), CompoundRenewalProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html.

Text

Wolfram Research (2012), CompoundRenewalProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html.

CMS

Wolfram Language. 2012. "CompoundRenewalProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html.

APA

Wolfram Language. (2012). CompoundRenewalProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html

BibTeX

@misc{reference.wolfram_2024_compoundrenewalprocess, author="Wolfram Research", title="{CompoundRenewalProcess}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_compoundrenewalprocess, organization={Wolfram Research}, title={CompoundRenewalProcess}, year={2012}, url={https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html}, note=[Accessed: 21-December-2024 ]}