ReverseGraph

ReverseGraph[g]

gives the reverse graph of the directed graph g.

ReverseGraph[{vw,…}]

uses rules vw to specify the graph g.

Details and Options

  • ReverseGraph is also known as transpose graph or converse graph.
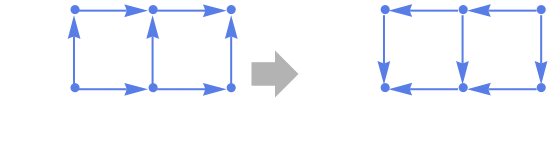
  • The reverse graph has the same vertices as g and the reverse edges.
  • ReverseGraph works with directed graphs, multigraphs, and mixed graphs.

Examples

open allclose all

Basic Examples  (1)

The reverse graph of a directed graph:

Scope  (6)

ReverseGraph does not affect undirected graphs:

ReverseGraph works with directed graphs:

Multigraphs:

Mixed graph:

Use rules to specify the graph:

ReverseGraph works with large graphs:

Properties & Relations  (3)

ReverseGraph has the same VertexList as the original graph:

ReverseGraph is equivalent to reversing edges:

The adjacency matrix of a reverse graph is the transpose of the matrix of the original graph:

Wolfram Research (2010), ReverseGraph, Wolfram Language function, https://reference.wolfram.com/language/ref/ReverseGraph.html (updated 2015).

Text

Wolfram Research (2010), ReverseGraph, Wolfram Language function, https://reference.wolfram.com/language/ref/ReverseGraph.html (updated 2015).

CMS

Wolfram Language. 2010. "ReverseGraph." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/ReverseGraph.html.

APA

Wolfram Language. (2010). ReverseGraph. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ReverseGraph.html

BibTeX

@misc{reference.wolfram_2024_reversegraph, author="Wolfram Research", title="{ReverseGraph}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/ReverseGraph.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_reversegraph, organization={Wolfram Research}, title={ReverseGraph}, year={2015}, url={https://reference.wolfram.com/language/ref/ReverseGraph.html}, note=[Accessed: 22-November-2024 ]}