ShiftedGompertzDistribution[λ,ξ]
尺度母数 λ,形状母数 ξ のシフトされたGompertz分布を表す.


ShiftedGompertzDistribution
ShiftedGompertzDistribution[λ,ξ]
尺度母数 λ,形状母数 ξ のシフトされたGompertz分布を表す.
詳細
- ShiftedGompertzDistributionは,時間とともに技術が採用される様子をモデル化するのに使われてきた.
- シフトされたGompertz分布中の値 x の累積分布関数は,
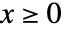 については
については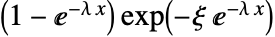 で与えられ,
で与えられ,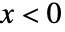 については0である.
については0である. - ShiftedGompertzDistributionでは,λ と ξ は任意の正の実数でよい.
- ShiftedGompertzDistributionでは,λ は任意の単位次元の数量でよく,ξ は無次元量でよい. »
- ShiftedGompertzDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
例題
すべて開く すべて閉じる例 (4)
スコープ (8)
シフトされたGompertz分布に従う擬似乱数のサンプルを生成する:
そのヒストグラムをPDFと比較する:
シフトされたGompertz分布の歪度は形状母数のみに依存する:
シフトされたGompertz分布の尖度は形状母数のみに依存する:
母数でQuantityを一貫して使うとQuantityDistributionが返される:
アプリケーション (3)
シフトされたGompertz分布を使ってソーシャルネットワーク内の関心事(例えばFacebookについてのGoogle検索の相対的な週ごとの数)をモデル化することができる:
データを切断されシフトされたGompertz分布にフィットする:
シフトされたGompertz分布は採用率 λ,母数 ξ で技術の採用までの時間のモデル化に使われる.これは,採用傾向と関連している:
このモデルにおける採用までの時間の中央値は ξ とともに大きくなり,λ とともに小さくなる:
採用のハザード率は,このモデルでは,技術普及の増加関数である:
採用傾向についての不均一集団について,採用までの時間はParameterMixtureDistributionによって減少する,指数混合分布は古典的なBassモデルを再現する:
Bassモデルでは,ハザード関数は技術の普及レベル(CDF)において線形である:
GammaDistributionの混合母数 ξ はガンマシフトされたGompertzモデルを与える:
ガンマシフトされたGompertzモデルについての技術採用までの時間の条件付き確率:
ガンマシフトGompertzモデル(GSG)は技術革新の採用モデル(例えば,連続時間区間におけるマンモグラフスキャナーの採用数)として使われる:
ビンに入れられたデータについて多項分布を考慮することで母数を推定し,LogLikelihoodを最大化する:
数値的不安定さを回避するために拡張WorkingPrecisionを使って母数を推定し,確実に収束するように最大反復回数を大きくする:
特性と関係 (3)
ExponentialDistributionおよびExtremeValueDistributionの最大値はShiftedGompertzDistributionに従う:
小さい形状母数 ξ の極限では,シフトされたGompertz分布は割合 λ で指数分布に収束する:
テキスト
Wolfram Research (2015), ShiftedGompertzDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/ShiftedGompertzDistribution.html (2016年に更新).
CMS
Wolfram Language. 2015. "ShiftedGompertzDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ShiftedGompertzDistribution.html.
APA
Wolfram Language. (2015). ShiftedGompertzDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ShiftedGompertzDistribution.html
BibTeX
@misc{reference.wolfram_2025_shiftedgompertzdistribution, author="Wolfram Research", title="{ShiftedGompertzDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ShiftedGompertzDistribution.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_shiftedgompertzdistribution, organization={Wolfram Research}, title={ShiftedGompertzDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/ShiftedGompertzDistribution.html}, note=[Accessed: 05-February-2026]}