ShiftedGompertzDistribution
ShiftedGompertzDistribution[λ,ξ]
表示尺度参数为 λ、形状参数为 ξ 的偏移 Gompertz 分布.
更多信息
- ShiftedGompertzDistribution 被广泛用于模拟技术随时间推移被采用的情况.
- 在偏移 Gompertz 分布中值 x 的累积分布函数在
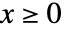 时,由
时,由 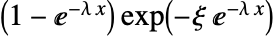 给出,在
给出,在 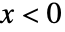 时为零.
时为零. - ShiftedGompertzDistribution 允许 λ 和 ξ 为任意正实数.
- ShiftedGompertzDistribution 允许 λ 为带有任意单位量纲的量,允许 ξ 为无量纲量. »
- ShiftedGompertzDistribution 可以与诸如 Mean、CDF 和 RandomVariate 等函数一起使用.
范例
打开所有单元关闭所有单元范围 (8)
比较其直方图与 PDF:
在参数中对 Quantity 一致的使用产生了 QuantityDistribution:
应用 (3)
The shifted偏移 Gompertz 分布可用于模拟社交网络兴趣的增长与衰减——例如,谷歌搜索脸书相对的每周的计数:
偏移 Gompertz 分布被用于模拟时间与技术采用的关系,其中采用率为 λ、参数为 ξ,与采用倾向相关:
对于与采用倾向相关的异构群体,采用时间由 ParameterMixtureDistribution 描述. 指数混合分布重现了经典 Bass 模型:
在 Bass 模型中,风险函数在技术渗透水平(CDF)中是线性的:
将参数 ξ 与 GammaDistribution 混合给出伽玛-偏移 Gompertz 分布模型:
对于伽玛-偏移 Gompertz 模型,技术被采用的时间的条件概率:
伽玛偏移 Gompertz 模型(GSG)可以用作创新被采用的模型——例如,乳腺放射成像扫描仪在连续时间间隔上被采用的次数:
通过考虑分组数据的多项式分布和对其 LogLikelihood 最大化进行参数估计:
使用扩展 WorkingPrecision 估计参数,以避免数值不稳定性;并提高迭代最大次数以确保收敛性:
属性和关系 (3)
ExponentialDistribution 的最大值和 ExtremeValueDistribution 服从ShiftedGompertzDistribution:
在较小的形状参数 ξ 的限制下,偏移 Gompertz 分布收敛于速率为 λ 的指数分布:
文本
Wolfram Research (2015),ShiftedGompertzDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ShiftedGompertzDistribution.html (更新于 2016 年).
CMS
Wolfram 语言. 2015. "ShiftedGompertzDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/ShiftedGompertzDistribution.html.
APA
Wolfram 语言. (2015). ShiftedGompertzDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ShiftedGompertzDistribution.html 年