WOLFRAM

Wolfram 语言与系统 参考资料中心
Wolfram 语言首页 »

SpheroidalJoiningFactor
✖
SpheroidalJoiningFactor

✖

给出 n 阶 m 次球面连接因子.

更多信息

范例

打开所有单元关闭所有单元

基本范例  (2)常见实例总结

数值运算：

In[1]:=1
✖
https://wolfram.com/xid/0e47wwz6am8dle-lwoon
Out[1]=1

在实数的子集上绘图：

In[1]:=1
✖
https://wolfram.com/xid/0e47wwz6am8dle-fcl9v1
Out[1]=1

范围  (9)标准用法实例范围调查

数值计算  (4)

数值计算：

In[1]:=1
✖
https://wolfram.com/xid/0e47wwz6am8dle-l274ju
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e47wwz6am8dle-whe1w
Out[2]=2

高精度计算：

In[1]:=1
✖
https://wolfram.com/xid/0e47wwz6am8dle-b0wt9
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e47wwz6am8dle-zn1q5
Out[2]=2

输出的精度与输入的精度一致：

In[3]:=3
✖
https://wolfram.com/xid/0e47wwz6am8dle-y7k4a
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0e47wwz6am8dle-hj5hh1
Out[4]=4

复数输入：

In[1]:=1
✖
https://wolfram.com/xid/0e47wwz6am8dle-hfml09
Out[1]=1

高精度条件下进行高效计算：

In[1]:=1
✖
https://wolfram.com/xid/0e47wwz6am8dle-jfkmzs
Out[1]=1
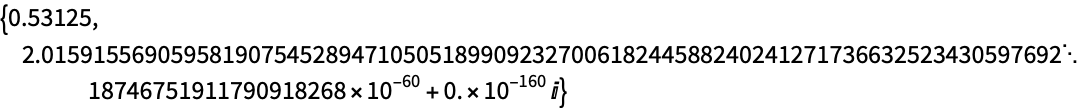
In[2]:=2
✖
https://wolfram.com/xid/0e47wwz6am8dle-g7yvq5
Out[2]=2

特殊值  (3)

零处的值：

In[1]:=1
✖
https://wolfram.com/xid/0e47wwz6am8dle-lssi7y
Out[1]=1

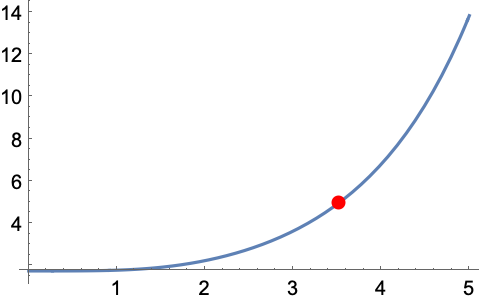
求满足 SpheroidalJoiningFactor[0,1/2,x]=5 的 x 值：

In[1]:=1
✖
https://wolfram.com/xid/0e47wwz6am8dle-f2hrld
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e47wwz6am8dle-eokm8z
Out[2]=2

SpheroidalJoiningFactor 逐项作用于列表的各个元素：

In[1]:=1
✖
https://wolfram.com/xid/0e47wwz6am8dle-bcfqi
Out[1]=1

可视化  (2)

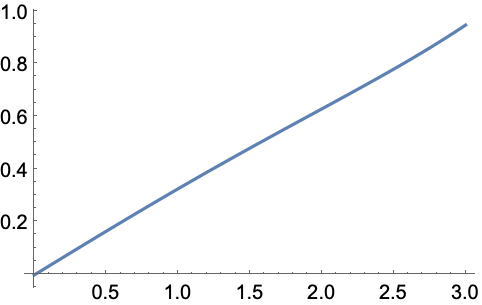
绘制 SpheroidalJoiningFactor 函数：

In[1]:=1
✖
https://wolfram.com/xid/0e47wwz6am8dle-tkgax
Out[1]=1

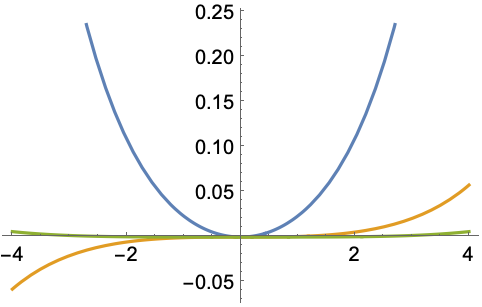
绘制 SpheroidalJoiningFactor[2,1,x+i y] 的实部：

In[1]:=1
✖
https://wolfram.com/xid/0e47wwz6am8dle-icstrk
Out[1]=1

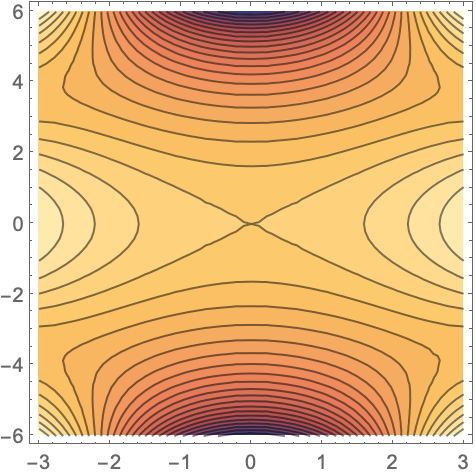
绘制 SpheroidalJoiningFactor[2,1,x+i y] 的虚部：

In[2]:=2
✖
https://wolfram.com/xid/0e47wwz6am8dle-hgtngl
Out[2]=2

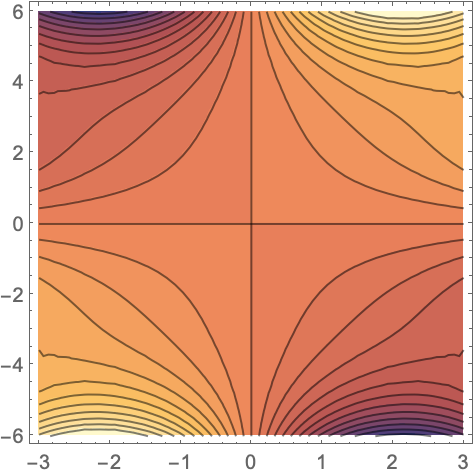
应用  (1)用该函数可以解决的问题范例

径向函数和角球体函数之间的关系：

In[1]:=1
✖
https://wolfram.com/xid/0e47wwz6am8dle-jsm3s7

代入数值进行检查：

In[2]:=2
✖
https://wolfram.com/xid/0e47wwz6am8dle-cskzvr
Out[2]=2

可能存在的问题  (1)常见隐患和异常行为

在 n 取半整数和 m 取一般值情况下，球体函数不进行计算：

In[1]:=1
✖
https://wolfram.com/xid/0e47wwz6am8dle-c6p1oc
Out[1]=1
Wolfram Research (2007)，SpheroidalJoiningFactor，Wolfram 语言函数，https://reference.wolfram.com/language/ref/SpheroidalJoiningFactor.html.
✖
Wolfram Research (2007)，SpheroidalJoiningFactor，Wolfram 语言函数，https://reference.wolfram.com/language/ref/SpheroidalJoiningFactor.html.

文本

Wolfram Research (2007)，SpheroidalJoiningFactor，Wolfram 语言函数，https://reference.wolfram.com/language/ref/SpheroidalJoiningFactor.html.

✖
Wolfram Research (2007)，SpheroidalJoiningFactor，Wolfram 语言函数，https://reference.wolfram.com/language/ref/SpheroidalJoiningFactor.html.

CMS

Wolfram 语言. 2007. "SpheroidalJoiningFactor." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SpheroidalJoiningFactor.html.

✖
Wolfram 语言. 2007. "SpheroidalJoiningFactor." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SpheroidalJoiningFactor.html.

APA

Wolfram 语言. (2007). SpheroidalJoiningFactor. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SpheroidalJoiningFactor.html 年

✖
Wolfram 语言. (2007). SpheroidalJoiningFactor. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SpheroidalJoiningFactor.html 年

BibTeX

@misc{reference.wolfram_2025_spheroidaljoiningfactor, author="Wolfram Research", title="{SpheroidalJoiningFactor}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/SpheroidalJoiningFactor.html}", note=[Accessed: 07-April-2025 ]}

✖
@misc{reference.wolfram_2025_spheroidaljoiningfactor, author="Wolfram Research", title="{SpheroidalJoiningFactor}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/SpheroidalJoiningFactor.html}", note=[Accessed: 07-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_spheroidaljoiningfactor, organization={Wolfram Research}, title={SpheroidalJoiningFactor}, year={2007}, url={https://reference.wolfram.com/language/ref/SpheroidalJoiningFactor.html}, note=[Accessed: 07-April-2025 ]}

✖
@online{reference.wolfram_2025_spheroidaljoiningfactor, organization={Wolfram Research}, title={SpheroidalJoiningFactor}, year={2007}, url={https://reference.wolfram.com/language/ref/SpheroidalJoiningFactor.html}, note=[Accessed: 07-April-2025 ]}