SplicedDistribution[{w1,w2,…,wn},{c0,c1,…,cn},{dist1,dist2,…,distn}]
represents the distribution obtained by splicing the distributions dist1, dist2, … truncated on the intervals {c0,c1}, {c1,c2}, … with weights w1, w2, … .


SplicedDistribution
SplicedDistribution[{w1,w2,…,wn},{c0,c1,…,cn},{dist1,dist2,…,distn}]
represents the distribution obtained by splicing the distributions dist1, dist2, … truncated on the intervals {c0,c1}, {c1,c2}, … with weights w1, w2, … .
Details
- SplicedDistribution is equivalent to MixtureDistribution[{w1,w2,…},{TruncatedDistribution[{c0,c1},dist1],…}].
- The distributions dist1, dist2, … need to be all continuous univariate distributions.
- The weights wi can be any non-negative real numbers.
- The interval limits
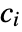 can be any real numbers such that
can be any real numbers such that 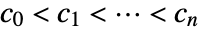 .
. - SplicedDistribution can be used with such functions as Mean, CDF, and RandomVariate, etc.
Examples
open all close allBasic Examples (2)
Scope (4)
Add symmetric exponential tails to normal distribution:
Since distribution is symmetric, all odd moments are 0:
Create a Student ![]() distribution with a heavier right tail:
distribution with a heavier right tail:
Generate a set of pseudorandom numbers that follow this distribution:
Compare the histogram of the sample to the PDF:
Generate a set of pseudorandom numbers following lognormal distribution with exponential tails:
Compare the histogram of the sample with the PDF:
Splicing QuantityDistribution with compatible units yields QuantityDistribution:
Applications (1)
Create a spliced distribution, with normal distribution in the center and tails of a heavy-tail distribution:
Find spliced distribution with continuous PDF by adjusting the weights:
Equate limits at both points of possible discontinuity:
Plot PDF of the spliced distribution:
Properties & Relations (3)
A spliced distribution is related to ProbabilityDistribution and TruncatedDistribution:
Represent as a linear combination of truncated PDFs:
A spliced distribution is related to MixtureDistribution and TruncatedDistribution:
Represent as a mixture of truncated distributions:
SplicedDistribution with one distribution simplifies to TruncatedDistribution:
Text
Wolfram Research (2012), SplicedDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/SplicedDistribution.html (updated 2016).
CMS
Wolfram Language. 2012. "SplicedDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/SplicedDistribution.html.
APA
Wolfram Language. (2012). SplicedDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SplicedDistribution.html
BibTeX
@misc{reference.wolfram_2025_spliceddistribution, author="Wolfram Research", title="{SplicedDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/SplicedDistribution.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_spliceddistribution, organization={Wolfram Research}, title={SplicedDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/SplicedDistribution.html}, note=[Accessed: 09-March-2026]}