SplicedDistribution[{w1,w2,…,wn},{c0,c1,…,cn},{dist1,dist2,…,distn}]
区間{c0,c1}, {c1,c2}, …で切断した分布 dist1, dist2, … をスプライスして得られた重み w1, w2, …の分布を表す.


SplicedDistribution
SplicedDistribution[{w1,w2,…,wn},{c0,c1,…,cn},{dist1,dist2,…,distn}]
区間{c0,c1}, {c1,c2}, …で切断した分布 dist1, dist2, … をスプライスして得られた重み w1, w2, …の分布を表す.
詳細
- SplicedDistributionはMixtureDistribution[{w1,w2,…},{TruncatedDistribution[{c0,c1},dist1],…}]に等しい.
- 分布 dist1, dist2, … はすべて一変量連続分布でなければならない.
- 重み wiは任意の非負の実数でよい.
- 区間限界
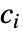 は
は 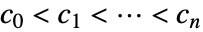 となる任意の実数でよい.
となる任意の実数でよい. - SplicedDistributionはMean,CDF,RandomVariate等の関数で使うことができる.
例題
すべて開く すべて閉じるスコープ (4)
指数関数的裾部がある正規対数分布に従う擬似乱数の集合を生成する:
互換的な単位でQuantityDistributionをスプライスすると QuantityDistributionが与えられる:
アプリケーション (1)
中心が正規分布,裾部が重い分布の裾部のスプライス分布を作る:
スプライスされた分布のPDFをプロットする:
特性と関係 (3)
繋ぎ合された分布はProbabilityDistributionおよびTruncatedDistributionに関連している:
繋ぎ合された分布はMixtureDistributionおよびTruncatedDistributionに関連している:
分布が1つのSplicedDistributionを簡約するとTruncatedDistributionになる:
関連するガイド
-
▪
- 保険数理で使われる分布 ▪
- 保険数理計算 ▪
- 派生統計分布
テキスト
Wolfram Research (2012), SplicedDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/SplicedDistribution.html (2016年に更新).
CMS
Wolfram Language. 2012. "SplicedDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/SplicedDistribution.html.
APA
Wolfram Language. (2012). SplicedDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SplicedDistribution.html
BibTeX
@misc{reference.wolfram_2025_spliceddistribution, author="Wolfram Research", title="{SplicedDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/SplicedDistribution.html}", note=[Accessed: 06-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_spliceddistribution, organization={Wolfram Research}, title={SplicedDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/SplicedDistribution.html}, note=[Accessed: 06-February-2026]}