SplicedDistribution
SplicedDistribution[{w1,w2,…,wn},{c0,c1,…,cn},{dist1,dist2,…,distn}]
表示通过拼接在区间 {c0,c1}, {c1,c2}, … 上截断的具有权值 w1, w2, … 的分布 dist1, dist2, … 得到的分布.
更多信息
- SplicedDistribution 等价于MixtureDistribution[{w1,w2,…},{TruncatedDistribution[{c0,c1},dist1],…}].
- 分布 dist1、dist2、… 必须全是连续单变量分布.
- 权值 wi 可以是任意非负实数.
- 区间极限
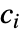 可以是满足
可以是满足 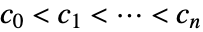 的任意实数.
的任意实数. - SplicedDistribution 可以与诸如 Mean、CDF 和 RandomVariate 等函数一起使用.
范例
打开所有单元关闭所有单元范围 (4)
将 QuantityDistribution 和相兼容的单位拼在一起生成 QuantityDistribution:
应用 (1)
属性和关系 (3)
拼接分布与 ProbabilityDistribution 和 TruncatedDistribution 相关:
拼接分布与 MixtureDistribution 和 TruncatedDistribution 相关:
具有一个分布的 SplicedDistribution 化简为 TruncatedDistribution:
文本
Wolfram Research (2012),SplicedDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SplicedDistribution.html (更新于 2016 年).
CMS
Wolfram 语言. 2012. "SplicedDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/SplicedDistribution.html.
APA
Wolfram 语言. (2012). SplicedDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SplicedDistribution.html 年