StationaryDistribution

StationaryDistribution[proc]

represents the stationary distribution of the process proc, when it exists.

Details

  • Stationary distribution is also known as limiting distribution, steady-state distribution, and invariant distribution.
  • The stationary distribution, if it exists, is a slice distribution that is independent of the time 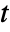and characterizes the limiting behavior of the process proc after all possible transients have vanished.
  • StationaryDistribution[proc] is equivalent to SliceDistribution[proc,∞].

Examples

open allclose all

Basic Examples  (1)

Stationary distribution for an M/M/1 queue:

Probability density function:

Mean and variance:

Compute the probability of an event:

Scope  (3)

Stationary distribution may autoevaluate to known distribution:

Stationary distribution may autoevaluate to a derived distribution:

Compute the stationary distribution for a discrete Markov process:

Some slice distributions:

Stationary distribution:

Visualize the convergence to the stationary distribution using the PDF:

Properties & Relations  (3)

Stationary distribution is the SliceDistribution at infinity:

The stationary distribution may depend on the initial state:

Mean system size is the mean of the stationary distribution for a queue:

Possible Issues  (1)

The stationary distribution may exist only for a certain range of process parameters:

Wolfram Research (2012), StationaryDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/StationaryDistribution.html.

Text

Wolfram Research (2012), StationaryDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/StationaryDistribution.html.

CMS

Wolfram Language. 2012. "StationaryDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/StationaryDistribution.html.

APA

Wolfram Language. (2012). StationaryDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StationaryDistribution.html

BibTeX

@misc{reference.wolfram_2024_stationarydistribution, author="Wolfram Research", title="{StationaryDistribution}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/StationaryDistribution.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_stationarydistribution, organization={Wolfram Research}, title={StationaryDistribution}, year={2012}, url={https://reference.wolfram.com/language/ref/StationaryDistribution.html}, note=[Accessed: 22-November-2024 ]}