WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

StationaryDistribution[proc]

過程 proc の定常分布があればそれを表す．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
特性と関係  
考えられる問題  
関連項目
関連するガイド
履歴
引用書式

StationaryDistribution

StationaryDistribution[proc]

過程 proc の定常分布があればそれを表す．

詳細

  • 定常分布は，極限分布，定常状態分布，不変分布としても知られている．
  • 定常分布は，それが存在する場合は，時間 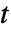に独立なスライス分布であり，可能なすべての過渡状態が消えた後の過程 proc の極限動作を特徴付ける．
  • StationaryDistribution[proc]はSliceDistribution[proc,∞]と等価である．

例題

すべて開く すべて閉じる

例  (1)

M/M/1待ち行列の定常分布：

Wolfram Language code: 𝒟 = StationaryDistribution[QueueingProcess[λ, μ]];

確率密度関数：

Wolfram Language code: PDF[𝒟, x]
Wolfram Language code: DiscretePlot[PDF[𝒟 /. {λ -> 5, μ -> 6}, x], {x, 0, 10}]

平均と分散：

Wolfram Language code: {Mean[𝒟], Variance[𝒟]}

ある事象の確率を計算する：

Wolfram Language code: Probability[x ^ 2 + E ^ x < 5, x𝒟]
Wolfram Language code: % /. {λ -> 5., μ -> 6}
Wolfram Language code: NProbability[x ^ 2 + E ^ x < 5, x𝒟 /. {λ -> 5, μ -> 6}]

スコープ  (3)

定常分布は既知の分布に自動評価されることがある：

Wolfram Language code: StationaryDistribution[OrnsteinUhlenbeckProcess[μ, σ, θ]]
Wolfram Language code: StationaryDistribution[OrnsteinUhlenbeckProcess[μ, σ, θ, Subscript[x, 0]]]
Wolfram Language code: StationaryDistribution[BernoulliProcess[p]]
Wolfram Language code: StationaryDistribution[DiscreteMarkovProcess[1, RotateRight /@ IdentityMatrix[3]]]

定常分布は派生分布に自動評価されることがある：

Wolfram Language code: StationaryDistribution[DiscreteMarkovProcess[1, With[{n = 10}, Table[Which[j == i - 1, i / n, j == i + 1, 1 - i / n, True, 0], {i, 0, n}, {j, 0, n}]]]]

離散マルコフ過程の定常分布を計算する：

Wolfram Language code: proc = DiscreteMarkovProcess[{1 / 3, 0, 2 / 3, 0, 0}, {{(1/2), (1/2), 0, 0, 0}, {(1/3), (2/3), 0, 0, 0}, {0, (1/3), (2/3), 0, 0}, {0, 0, 0, 0, 1}, {0, 0, 0, 1, 0}}];

いくつかのスライス分布：

Wolfram Language code: Table[N@PDF[proc[n], x], {n, {0, 3, 7, 12, 17}}]//Column

定常分布：

Wolfram Language code: StationaryDistribution[proc]

PDFを使って定常分布への収束を可視化する：

Wolfram Language code: DiscretePlot[PDF[proc[n], Range[5]], {n, 0, 20}, ExtentSize -> 1 / 3, ColorFunction -> Function[{x, y}, ColorData["Rainbow"][x]], AxesLabel -> {n, None}]

特性と関係  (3)

定常分布は無限大においてSliceDistributionである：

Wolfram Language code: StationaryDistribution[OrnsteinUhlenbeckProcess[μ, σ, θ, Subscript[x, 0]]]
Wolfram Language code: SliceDistribution[OrnsteinUhlenbeckProcess[μ, σ, θ, Subscript[x, 0]], ∞]

定常分布は初期状態に依存することがある：

Wolfram Language code: m = {{1 / 2, 1 / 2, 0, 0, 0}, {1 / 3, 2 / 3, 0, 0, 0}, {0, 1 / 3, 2 / 3, 0, 0}, {0, 0, 0, 0, 1}, {0, 0, 0, 1, 0}};
Wolfram Language code: StationaryDistribution[DiscreteMarkovProcess[1, m]]
Wolfram Language code: StationaryDistribution[DiscreteMarkovProcess[4, m]]

系の大きさの平均値は待ち行列の定常分布の平均値である：

Wolfram Language code: 𝒬 = QueueingProcess[λ, μ];
Wolfram Language code: QueueProperties[𝒬, "MeanSystemSize"]//Together
Wolfram Language code: Mean[StationaryDistribution[𝒬]]

考えられる問題  (1)

定常分布は過程の母数のある一定の範囲についてのみ存在することがある：

Wolfram Language code: QueueProperties[QueueingProcess[λ, μ], "StationarySystem"]
Wolfram Research (2012), StationaryDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/StationaryDistribution.html.

テキスト

Wolfram Research (2012), StationaryDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/StationaryDistribution.html.

CMS

Wolfram Language. 2012. "StationaryDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/StationaryDistribution.html.

APA

Wolfram Language. (2012). StationaryDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StationaryDistribution.html

BibTeX

@misc{reference.wolfram_2026_stationarydistribution, author="Wolfram Research", title="{StationaryDistribution}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/StationaryDistribution.html}", note=[Accessed: 16-June-2026]}

BibLaTeX

@online{reference.wolfram_2026_stationarydistribution, organization={Wolfram Research}, title={StationaryDistribution}, year={2012}, url={https://reference.wolfram.com/language/ref/StationaryDistribution.html}, note=[Accessed: 16-June-2026]}