WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

StirlingS1[n,m]

第1種スターリング(Stirling)数 TemplateBox[{n, m}, StirlingS1]を与える．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
アプリケーション  
特性と関係  
考えられる問題  
おもしろい例題  
関連項目
テクニカルノート
関連するガイド
関連リンク
履歴
引用書式

StirlingS1

StirlingS1[n,m]

第1種スターリング(Stirling)数 TemplateBox[{n, m}, StirlingS1]を与える．

詳細

  • 記号操作・数値操作の両方に適した数学的整数関数である．
  • StirlingS1は離散微積分のFactorialPowerから連続微積分 TemplateBox[{x, m}, FactorialPower]=sum_(m=1)^n TemplateBox[{n, m}, StirlingS1]x^mのPowerへの変換行列として定義される．ここで，m,n in TemplateBox[{}, PositiveIntegers]である．
  • (-1)^(n-m)TemplateBox[{n, m}, StirlingS1]は，厳密に 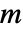個の巡回を含む 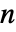個の要素の置換数を与える． »
  • StirlingS1は，自動的にリストに縫い込まれる．

例題

すべて開く すべて閉じる

例  (1)

第1種スターリング数を評価する：

複数のスターリング数を評価する：

スコープ  (2)

StirlingS1はリストに対して要素単位で適用される：

TraditionalFormによる表示：

アプリケーション  (5)

対数目盛で第1種スターリング数をプロットする：

2を法としたスターリング数：

n 個の要素のすべての置換の互いに素な巡回表現を生成する：

1, 2, … n 個のp互いに素な巡回を持つ置換の数を数える：

符号がない第1種スターリング数は互いに素な巡回の数を数える：

対称群要素における巡回の平均数をプロットする：

無限数列であり，独立同分布に従う連続確率変数の 番目の記録の位置の分布：

2番目の記録の確率質量関数を可視化する：

指定されたベクトルで 番目の記録位置を，それがあれば求めるコード：

ランダムな指数列中の2番目の記録の位置を計算し，そのヒストグラムを期待される確率質量関数と比較する：

特性と関係  (5)

通常型母関数で値を生成する：

指数型生成関数から値を生成する：

第1種スターリング数は，事実上第2種スターリング数の逆数である：

コーシー(Cauchy)の定理を用いて第1種スターリング数の大きいものを計算する：

第1種スターリング数は符号交互の階乗引数を伴う偏ベル多項式によって与えられる：

考えられる問題  (2)

StirlingS1は，中規模の引数に対して大きい値を持つことがある：

における値は1と定義されている：

おもしろい例題  (2)

各桁の数字の和をプロットする：

スターリング数の成分がある行列の行列式：

閉じた形と比較する：

Wolfram Research (1988), StirlingS1, Wolfram言語関数， https://reference.wolfram.com/language/ref/StirlingS1.html.

テキスト

Wolfram Research (1988), StirlingS1, Wolfram言語関数， https://reference.wolfram.com/language/ref/StirlingS1.html.

CMS

Wolfram Language. 1988. "StirlingS1." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/StirlingS1.html.

APA

Wolfram Language. (1988). StirlingS1. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StirlingS1.html

BibTeX

@misc{reference.wolfram_2025_stirlings1, author="Wolfram Research", title="{StirlingS1}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/StirlingS1.html}", note=[Accessed: 30-October-2025]}

BibLaTeX

@online{reference.wolfram_2025_stirlings1, organization={Wolfram Research}, title={StirlingS1}, year={1988}, url={https://reference.wolfram.com/language/ref/StirlingS1.html}, note=[Accessed: 30-October-2025]}