SystemModelLinearize[model]
给出均衡 model 的线性化的 StateSpaceModel.
SystemModelLinearize[model,op]
在运算点 op 处进行线性化.


SystemModelLinearize
SystemModelLinearize[model]
给出均衡 model 的线性化的 StateSpaceModel.
SystemModelLinearize[model,op]
在运算点 op 处进行线性化.
更多信息和选项


- SystemModelLinearize 给出运算点附近 model 的线性近似.
- 线性模型一般用于控制设计、优化和频率分析.
- 带有方程
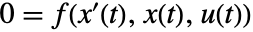 和输出方程
和输出方程 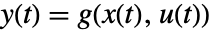 的系统在操作点
的系统在操作点 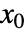 和
和 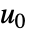 被线性化应该满足 f(0,x0,u0)0.
被线性化应该满足 f(0,x0,u0)0. - 返回的线性 StateSpaceModel 具有状态
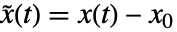 ,输入
,输入 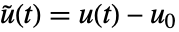 和输出
和输出 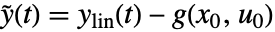 ,其中状态方程
,其中状态方程 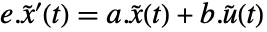 和输出方程
和输出方程 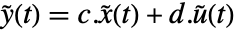 . 矩阵由
. 矩阵由 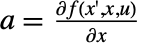 、
、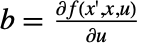 、
、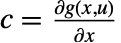 、
、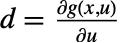 和
和 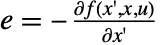 给出,均在
给出,均在 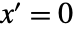 、
、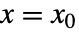 和
和 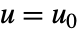 处计算.
处计算. - SystemModelLinearize[model] 等价于 SystemModelLinearize[model,"EquilibriumValues"].
- op 的规范为运算点使用以下值:
-
"InitialValues" 来自 model 的初始值 "EquilibriumValues" FindSystemModelEquilibrium[model] sim or {sim,"StopTime"} 来自 SystemModelSimulationData sim 的最终值 {sim,"StartTime"} sim 的初始值 {sim,time} 来自 sim 在 time 的值 {{{x1,x10},…},{{u1,u10},…}} 状态值 xi0 和输入值 ui0 - 可以使用 SystemModelSimulate[model,All,…] 获取仿真 sim.
- SystemModelLinearize 符号线性化 DAE 系统,或首先简化为 ODE 系统并数值化线性 ODE 结果.
- 可给出以下选项:
-
Method Automatic 线性化算法的方法 ProgressReporting $ProgressReporting 控制进程的显示 - Method 选项有以下可能的设置:
-
"NumericDerivative" 简化为 ODE,然后数值线性化 "SymbolicDerivative" 来自 DAE 系统的符号线性化 - Method{"SymbolicDerivative","ReduceIndex"False} 关闭指标约简.
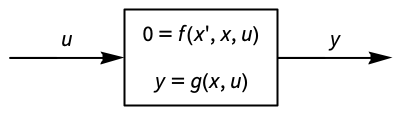
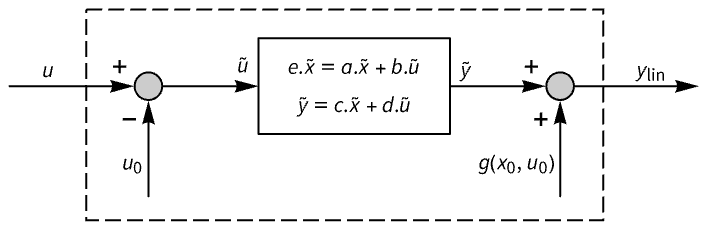
范例
打开所有单元 关闭所有单元基本范例 (3)
范围 (19)
线性化值 (5)
推广和延伸 (1)
隐藏所得 StateSpaceModel 中的标签:
选项 (5)
Method (4)
"SymbolicDerivative" 方法使用来自于仿真的完全指定的运算点:
"NumericDerivative" 方法使用由状态和输入点指定的运算点:
用 "ReduceIndex" 在符号线性化时关闭指标约简:
关闭指标约简得到一个描述 StateSpaceModel:
ProgressReporting (1)
用 ProgressReporting 控制进度汇报:
应用 (10)
分析线性系统 (5)
对仿真数据使用 Fourier 以验证结果:
属性和关系 (8)
使用 SystemModel 的属性在初值点进行线性化:
用 FindSystemModelEquilibrium 在平衡点进行线性化:
用 TransferFunctionModel 转换为传递函数表示:
用 ToDiscreteTimeModel 离散化线性化模型:
StateSpaceModel 可以线性化常微分方程组:
用 SystemModelLinearize 线性化同一系统的 SystemModel:
根据方程创建一个 NonlinearStateSpaceModel,并与 SystemModel 相比较:
文本
Wolfram Research (2018),SystemModelLinearize,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SystemModelLinearize.html (更新于 2020 年).
CMS
Wolfram 语言. 2018. "SystemModelLinearize." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/ref/SystemModelLinearize.html.
APA
Wolfram 语言. (2018). SystemModelLinearize. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SystemModelLinearize.html 年
BibTeX
@misc{reference.wolfram_2025_systemmodellinearize, author="Wolfram Research", title="{SystemModelLinearize}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/SystemModelLinearize.html}", note=[Accessed: 17-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_systemmodellinearize, organization={Wolfram Research}, title={SystemModelLinearize}, year={2020}, url={https://reference.wolfram.com/language/ref/SystemModelLinearize.html}, note=[Accessed: 17-February-2026]}

