SystemsModelDelay 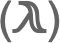
表示 StateSpaceModel 或者 TransferFunctionModel 中的时间延迟 δ.
更多信息

- SystemsModelDelay[δ] 使表示涉及时间延迟的系统成为可能,并且有效地操作、近似和模拟这些系统.
- SystemsModelDelay[δ] 在 StandardForm 中为 δ,并且可以以使用
 delay
delay 输入.
输入. - 对于 StateSpaceModel,SystemsModelDelay[δ] 可以线性出现在任意系统矩阵中. 对于信号
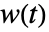 , SystemsModelDelay[δ]w[t] 为
, SystemsModelDelay[δ]w[t] 为 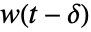 .
. - 对于 TransferFunctionModel,SystemsModelDelay[δ] 可以线性出现在多项式的系数中. 它表示变换时间延迟:
-
-δ s 连续时间系统中 z-δ 离散时间系统中 - 这里,s 是拉普拉斯变换变量,而 z 是 z 变换变量.
- 对于离散时间系统,延迟 δ 是 SamplingPeriod 倍数.
范例
打开所有单元关闭所有单元范围 (7)
来自包含 SystemsModelDelay 的微分方程的离散时间系统:
属性和关系 (5)
Wolfram Research (2012),SystemsModelDelay,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SystemsModelDelay.html.
文本
Wolfram Research (2012),SystemsModelDelay,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SystemsModelDelay.html.
CMS
Wolfram 语言. 2012. "SystemsModelDelay." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SystemsModelDelay.html.
APA
Wolfram 语言. (2012). SystemsModelDelay. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SystemsModelDelay.html 年