TensorWedge

TensorWedge[tensor1,tensor2,…]

represents the antisymmetrized tensor product of the tensori.

Details

  • TensorWedge[a,b] can be input as ab. The character is entered as t^ or \[TensorWedge].
  • In a tensor wedge product of explicit or symbolic arrays, all slots must have the same dimension 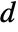, though different arrays may have different ranks. TensorWedge generalizes Cross, which requires 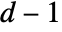vectors of length .
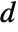  • The TensorWedge product of several arrays is an antisymmetric array, always given in SymmetrizedArray form.
  • If the tensors tensori are not antisymmetric, then they are effectively antisymmetrized before performing the product. Vectors are considered antisymmetric tensors of rank 1. Scalars are considered antisymmetric tensors of rank 0.
  • The wedge product TensorWedge[t1,…,tk] of the antisymmetric tensors ti is equivalent to Multinomial[r1,…,rk]*Symmetrize[TensorProduct[t1,…,tk],Antisymmetric[All]], where ri is the tensor rank of ti.

Examples

open allclose all

Basic Examples  (1)

Antisymmetrized tensor product of explicit vectors:

In normal form:

Scope  (3)

Wedge product of vectors:

Wedge product of antisymmetric arrays:

Wedge product of symbolic arrays:

Properties & Relations  (11)

The wedge product is anticommutative for vectors:

The wedge product is commutative for matrices:

The result is always antisymmetric:

The wedge product is associative:

The tensor wedge product of a single array is equivalent to its antisymmetrization:

The Hodge dual of the wedge product of vectors in dimension coincides with the cross product of those vectors:

The wedge product requires all arguments to have slots of the same dimension, but ranks can be arbitrary:

The result is always antisymmetric:

Take two arrays in dimension , say :

If the total rank of the wedge product is larger than the dimension , then that product is 0:

The wedge product of an array of odd rank with itself is zero:

But if the rank is even, then the result is not a zero array:

With symbolic arrays:

The wedge product is proportional to antisymmetrization of the tensor product:

The proportionality factor is the Multinomial of the ranks:

For vectors of length , the only independent component of their TensorWedge equals the determinant of the list of those vectors:

The tensor wedge product is linear in all its arguments:

Possible Issues  (1)

TensorWedge has attribute OneIdentity. However TensorWedge[t] is equivalent to t only for an antisymmetric tensor t:

Antisymmetry in only some slots is not enough:

Wolfram Research (2012), TensorWedge, Wolfram Language function, https://reference.wolfram.com/language/ref/TensorWedge.html.

Text

Wolfram Research (2012), TensorWedge, Wolfram Language function, https://reference.wolfram.com/language/ref/TensorWedge.html.

CMS

Wolfram Language. 2012. "TensorWedge." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TensorWedge.html.

APA

Wolfram Language. (2012). TensorWedge. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TensorWedge.html

BibTeX

@misc{reference.wolfram_2024_tensorwedge, author="Wolfram Research", title="{TensorWedge}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/TensorWedge.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_tensorwedge, organization={Wolfram Research}, title={TensorWedge}, year={2012}, url={https://reference.wolfram.com/language/ref/TensorWedge.html}, note=[Accessed: 22-December-2024 ]}