TimeValue
TimeValue[s,i,t]
按利率 i 计算证券 s 在时间 t 的价值.
更多信息和选项


- 对于简单量 a 和正的时间 t,TimeValue[a, i, t] 给出 a 在 t 时刻、实际利率为 i 的情况下的未来值或累积值. »
- 对于简单量 a 和负的时间 t,TimeValue[a, i, t] 出 a 在实际利率为 i 的情况下当前的值或贴现值. »
- TimeValue 适用于任意数字或符号表达式. 对于 TimeValue 返回的符号公式,可通过 Solve 和 FindRoot 等内置函数求利率、支付或时间段.
- 证券 s 可以采用以下其他形式和解释:
-
Annuity 时间段末期的一系列付款 AnnuityDue 时间段初期的一系列付款 Cashflow 现金流 » - TimeValue[Annuity[…],interest,t] 计算年金在时间 t 一次性支付的价值. 可能的年金计算包括抵押贷款估值、债券定价和付款或收益率计算.
- TimeValue[Cashflow[…],interest,t] 计算现金流在时间 t 一次性等价支付的价值. 可能的现金流计算包括净现值、贴现现金流和内部收益率.
- TimeValue[s,i,{t,t1}] 以利率 i 计算从 t1 到 t 累计或贴现的值. 时间 t1 为现金流起始的参考点. »
- TimeValue[s,i] 等价于 TimeValue[s,i,0].
- TimeValue[…,t] 等价于 TimeValue[…,{t,0}].
- 在 TimeValue[s,i,t] 中,利率 i 可以用下列形式指定:
-
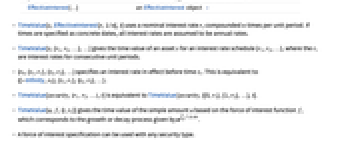
r 实际利率 {r1,r2,…} 单位时间间隔内应用的利率表 » {{t1,r1},{t2,r2},…} 在指定时间发生变化的利率表 » {p1->r1,p2->r2,…} 实际利率的期限结构 » function 利息力,以时间的函数的形式给出 » EffectiveInterest[…] EffectiveInterest 对象 » - TimeValue[s,EffectiveInterest[r,1/n],t] 使用名义利率 r,每个单位期间复合 n 次. 如果时间为具体日期,则假定所有利率为年利率.
- TimeValue[s,{r1,r2,…},…] 给出资产 s 在利率表 {r1,r2,…} 条件下的时间价值,其中 ri 为连续单位期间的利率.
- {r0,{t1,r1},{t2,r2},…} 指定 t1 时刻之前的实际利率. 这等价于 {{-Infinity,r0},{t1,r1},{t2,r2},…}.
- TimeValue[security,{r1,r2,…},t] 等价于 TimeValue[security,{{0,r1},{1,r2},…},t].
- TimeValue[a,f,{t,t1}] 根据利息函数 f 给出金额 a 的在某个时间的值,对应于增长或减少过程
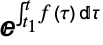 .
. - 利息力指标可用于任何债券类型.
- 可以给出下列选项:
-
Assumptions $Assumptions 关于参数的假设 GenerateConditions False 是否生成关于参数的条件
范例
打开所有单元关闭所有单元基本范例 (10)
范围 (14)
应用 (15)
求在年利率9%时,如果要在三年底得到$1000,必须投资的数额:
已知半年复利,利率为6%,求$1000累加到$1500所需要的时间:
已知实际利率在第一个五年为 r1,第二个五年为 r2,第三个五年为 r3,求$1000在15年末累加值的表达式:
在按季复利、年利率为8%的条件下,一个人投资$1000,求此人在每个季度末能取出多少,才能在10年底正好把这笔资金用完:
在按季复利条件下,如果每个季度末付款$1000,连续付款5年,所得到的现值为$16000,求利率:
已知每年支付$100,前六年的实际利率为5%,后四年的实际利率为4%. 求一个10年期年金的累加值:
为了在第8年末得到$600,某人现立即支付$100,在第5年末支付$200,并在第10年末进行最后一笔支付. 求最后一笔支付为多少才能使他的投资回报率等于8%(半年复利):
有$100、$200 和$500的付款分别要在第 2、3 和 8 年末支付. 求$800的付款在5%利率时与之等价所在的时间点:
在实际利率为何值时,$2000在第2年末的现值加上$3000在第4年末的现值等于$4000:
由于一笔贷款余额在任何时间都等于其剩余的未来付款的现值,Annuity 可用于创建分期偿还表:
属性和关系 (2)
可能存在的问题 (3)
在求解长期或高频率年金或债券的利率时,可能需要用 FindRoot,而不是 Solve:
为了使 TimeValue 确定一组利率表中的利率是否满足估计时间段,估值时间段必须为数值型:
用 TimeSeries 指定汇率要求初始时间为0:
互动范例 (1)
利用 Manipulate 研究一组现金流与一组变量之间的各种依存关系:
文本
Wolfram Research (2010),TimeValue,Wolfram 语言函数,https://reference.wolfram.com/language/ref/TimeValue.html (更新于 2024 年).
CMS
Wolfram 语言. 2010. "TimeValue." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/TimeValue.html.
APA
Wolfram 语言. (2010). TimeValue. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/TimeValue.html 年