WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

UnitaryMatrix

UnitaryMatrix[umat]

ユニタリ行列 umat を構造化配列に変換する．

詳細とオプション

ユニタリ行列は，構造化配列として表されているときは，便利に指定でき，InverseやLinearSolveを含む操作もより効率的になる．
ユニタリ行列を使う行列分解には，QR分解，ヘッセンベルク(Hessenberg)分解，シューア(Schur)分解，特異値分解がある．
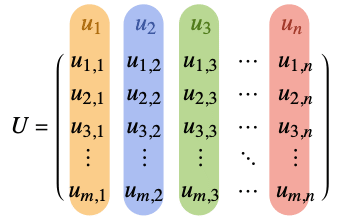
ユニタリ行列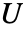の列ベクトル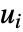は正規直行なので， $TemplateBox[{{u, _, i}}, Conjugate].u_j=TemplateBox[{{i, ,, j}}, KroneckerDeltaSeq]$ である．

正方ユニタリ行列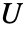は共役転置がその逆と等しい行列である．つまり，関係を満足する行列である．
ユニタリ行列の逆行列もまたユニタリ行列である．
次元 p×q の行列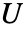は，p≥q でが q×q 固有行列か p≤q でが p×p 固有行列なら正行列である．
ユニタリ行列は行列の乗算の下で閉じているので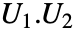，もまたユニタリ行列である．
UnitaryMatrix sa の次の特性"prop"には sa["prop"]でアクセスすることができる．

	"Matrix"	完全配列として表されたユニタリ行列
	"Properties"	サポートされる特性のリスト
	"Structure"	構造化配列の型
	"StructuredData"	構造化配列に保存された内部データ
	"StructuredAlgorithms"	構造化配列についての特別なメソッドを持つ関数のリスト
	"Summary"	Datasetとして表された要約情報

Normal[UnitaryMatrix[…]]はユニタリ行列を通常の行列として与える．
UnitaryMatrix[…,TargetStructure->struct]はユニタリ行列を struct で指定された形式で返す．次は，可能な設定である．
Automatic 返す表現を自動的に選択する

"Dense" 行列を密な行列として表す

"Structured" 行列を構造化配列として表す
UnitaryMatrix[…,TargetStructureAutomatic]はUnitaryMatrix[…,TargetStructure"Structured"]に等しい．

例題

すべて開くすべて閉じる

例 (1)

ユニタリ行列を構築する：

要素を表示する：

NormalはUnitaryMatrixを通常の表現に変換できる：

スコープ (3)

複素反射行列は，ユニタリ行列でもありエルミート行列でもある：

矩形ユニタリ行列：

その共役転置もまたユニタリ行列である：

UnitaryMatrixオブジェクトは行列についての情報を与える特性を含む：

"Summary"特性は行列についての情報の簡単な要約を与える：

"StructuredAlgorithms"特性は構造化アルゴリズムを持つ関数をリストにする：

オプション (1)

TargetStructure (1)

ユニタリ行列を密な行列として返す：

ユニタリ行列を構造化配列として返す：

アプリケーション (5)

CircularUnitaryMatrixDistributionから導かれた行列はユニタリ行列である：

CircularOrthogonalMatrixDistributionから導かれた行列はユニタリ行列である：

パウリ(Pauli)行列はユニタリ行列である：

指数行列もまたユニタリ行列である：

ユニタリ行列は $TemplateBox[{}, Complexes]^n$ 上で標準的な内積を保持する．表現を変えるなら，がユニタリ行列でとはベクトルなら，である：

これは，ベクトル間の角度が変わらないことを意味する：

ノルムは内積から派生するので，ノルムもまた保持される：

ユニタリ行列は多くの行列分解で重要な役割を果たす：

行列 $H_v=I_n-(2 vTemplateBox[{v}, Conjugate])/(v.TemplateBox[{v}, Conjugate])$ は，任意の非零のベクトルについて常にユニタリ行列である：

はハウスホルダー(Householder)反射と呼ばれる．純粋な反射なので，その行列式はである：

これはと垂直な平面を通る反射で，をに送る：

に垂直な任意のベクトルはによって変更されない：

行列計算において，は指定された列ベクトルの選択された成分を0に設定するために使用される：

特性と関係 (2)

UnitaryMatrixの共役転置はもとの行列の逆行列に等しい：

実数直交行列はユニタリ行列でもある：

トップへ