VarianceEstimatorFunction

VarianceEstimatorFunction

LinearModelFitおよびNonlinearModelFitのオプションで，分散推定量を指定する．

詳細

  • VarianceEstimatorFunctionは，誤差が正規分布に従うと推定できる線形および非線形モデルの誤差分散のスケールを推定する関数を定義する．
  • VarianceEstimatorFunction->f と設定すると，分散のスケールは f[res,w] で推定される．ただし，res={y1-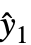,y2-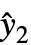,…} は残差のリスト，w はWeightsオプションの設定で指定される重みのリストである．
  • デフォルト設定のAutomaticでは，分散スケールは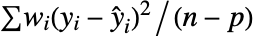で推定される．ただし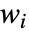，は 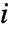番目のデータ点の重み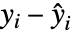，は 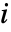番目の残差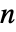， データ要素の数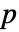， はモデル中のパラメータの数である．
  • VarianceEstimatorFunction->(1&)とWeights->{1/Δy12,1/Δy22,…}では，Δyiは尺度 yiの既知の不確実性であるとして扱われ，パラメータの標準誤差は重みだけから計算される． »

例題

すべて開くすべて閉じる

例  (1)

誤差分散でデフォルトの不変推定値を使う：

既知の誤差分散を仮定する：

平均平方誤差で分散を推定する：

スコープ  (2)

FittedModel内で推定を定義する：

非線形モデルとともに使う：

平均絶対誤差で分散を推定する：

アプリケーション  (1)

測定誤差を重みとして使って非線形モデルをフィットする：

共通の誤差のスケールを1で推定する：

パラメータの標準誤差を得る：

デフォルトの分散推定を使って推定と比較する：

特性と関係  (1)

誤差推定と信頼区間は分散推定を含む：

デフォルトの推測子を使う：

単位誤差スケールを想定する：

平均平方誤差で推定する：

Wolfram Research (2008), VarianceEstimatorFunction, Wolfram言語関数， https://reference.wolfram.com/language/ref/VarianceEstimatorFunction.html.

テキスト

Wolfram Research (2008), VarianceEstimatorFunction, Wolfram言語関数， https://reference.wolfram.com/language/ref/VarianceEstimatorFunction.html.

CMS

Wolfram Language. 2008. "VarianceEstimatorFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/VarianceEstimatorFunction.html.

APA

Wolfram Language. (2008). VarianceEstimatorFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VarianceEstimatorFunction.html

BibTeX

@misc{reference.wolfram_2024_varianceestimatorfunction, author="Wolfram Research", title="{VarianceEstimatorFunction}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/VarianceEstimatorFunction.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_varianceestimatorfunction, organization={Wolfram Research}, title={VarianceEstimatorFunction}, year={2008}, url={https://reference.wolfram.com/language/ref/VarianceEstimatorFunction.html}, note=[Accessed: 22-November-2024 ]}