VectorLessEqual 
xy または VectorLessEqual[{x,y}]
![]() のすべての成分について xi≤yiなら,長さ n のベクトルに対してTrueを返す.
のすべての成分について xi≤yiなら,長さ n のベクトルに対してTrueを返す.
xκy または VectorLessEqual[{x,y},κ]
y-x∈κ なら,x と y とに対してTrueを返す.ただし,κ は真凸錐である.
詳細


- VectorLessEqualは,ベクトル空間演算と互換の,
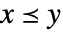 および
および 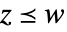 がすべての
がすべての 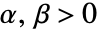 について
について 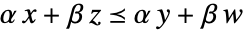 を意味する,ベクトル,行列,配列の半順序を与える.
を意味する,ベクトル,行列,配列の半順序を与える. - VectorLessEqualは,制約条件付き最適化,不等式の解法,積分におけるベクトル不等式を指定するのに使われることが多い.これは,ベクトル最適化における極小元の定義にも使われる.
- x および y が
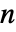 -ベクトルのとき,xy は
-ベクトルのとき,xy は  に等しい.この関係が真となるためには,x の各部分は対応する y の部分以下でなければならない.
に等しい.この関係が真となるためには,x の各部分は対応する y の部分以下でなければならない. - x および y が次元
 の配列のとき,xy は
の配列のとき,xy は 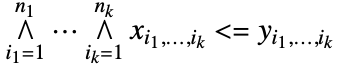 に等しい.この関係が真となるためには,x の各部分は対応する y の部分以下でなければならない.
に等しい.この関係が真となるためには,x の各部分は対応する y の部分以下でなければならない. - x または y が非数値要素を持つとき,xy は未評価のままになる.それ以外の場合は,一般にTrueまたはFalseを与える.
- x が n-ベクトルで y が数値スカラーのとき,
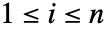 のすべての成分に対して xi≤y なら xy はTrueを与える.
のすべての成分に対して xi≤y なら xy はTrueを与える. - 記号 は
 v<=
v<= または \[VectorLessEqual]として入力する.下付き文字があるベクトル不等式は以下のように入力できる.
または \[VectorLessEqual]として入力する.下付き文字があるベクトル不等式は以下のように入力できる. -
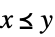
VectorLessEqual[{x,y}] 標準的ベクトル不等式 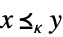
VectorLessEqual[{x,y},κ] 錐体 κ によって定義されるベクトル不等式 - 一般に,適切な真凸錐 κ を使ってベクトル不等式を指定することができる.集合
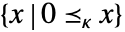 は κ と同じである.
は κ と同じである. - ベクトル x についての
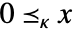 のときの可能な錐体指定 κ には以下がある.
のときの可能な錐体指定 κ には以下がある. -
{"NonNegativeCone", n} ![TemplateBox[{n}, NonNegativeConeList] TemplateBox[{n}, NonNegativeConeList]](Files/VectorLessEqual.ja/21.png)
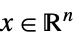 (
(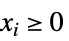 )
){"NormCone", n} ![TemplateBox[{n}, NormConeList] TemplateBox[{n}, NormConeList]](Files/VectorLessEqual.ja/24.png)
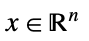 (Norm[{x1,…,xn-1}]≤xn)
(Norm[{x1,…,xn-1}]≤xn)"ExponentialCone" ![TemplateBox[{}, ExponentialConeString] TemplateBox[{}, ExponentialConeString]](Files/VectorLessEqual.ja/26.png)
 (
(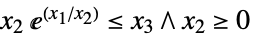 )
)"DualExponentialCone" ![TemplateBox[{}, DualExponentialConeString] TemplateBox[{}, DualExponentialConeString]](Files/VectorLessEqual.ja/29.png)
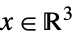 (
(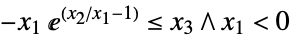 または
または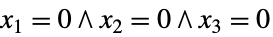 )
){"PowerCone",α} ![TemplateBox[{alpha}, PowerConeList] TemplateBox[{alpha}, PowerConeList]](Files/VectorLessEqual.ja/33.png)
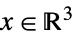 (
(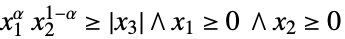 )
){"DualPowerCone",α} ![TemplateBox[{alpha}, DualPowerConeList] TemplateBox[{alpha}, DualPowerConeList]](Files/VectorLessEqual.ja/36.png)
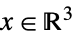 (
(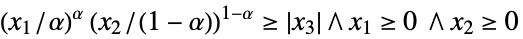 )
) - 行列 x についての
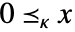 のときの可能な錐体指定 κ には以下がある.
のときの可能な錐体指定 κ には以下がある. -
"NonNegativeCone" ![TemplateBox[{}, NonNegativeConeString] TemplateBox[{}, NonNegativeConeString]](Files/VectorLessEqual.ja/40.png)
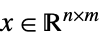 (
(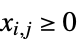 )
){"SemidefiniteCone", n} ![TemplateBox[{n}, SemidefiniteConeList] TemplateBox[{n}, SemidefiniteConeList]](Files/VectorLessEqual.ja/43.png)
対称半正定値行列 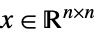
- 配列 x についての
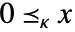 のときの可能な錐体指定 κ には以下がある.
のときの可能な錐体指定 κ には以下がある. -
"NonNegativeCone" ![TemplateBox[{}, NonNegativeConeString] TemplateBox[{}, NonNegativeConeString]](Files/VectorLessEqual.ja/46.png)
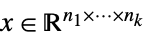 (
(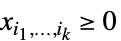 )
) - 厳密な数量については,VectorLessEqualは内部的に数値近似を使って数値順を確立する.この過程は大域変数$MaxExtraPrecisionの設定の影響を受けることがある.
例題
すべて開くすべて閉じる例 (3)
スコープ (7)
Norm[{x,y}]<=1という条件を表す:
アプリケーション (8)
基本的なアプリケーション (1)
VectorLessEqualは多くの要素を比較する高速の方法である:
ベクトル不等式上の最適化 (1)
ベクトル不等式を解く (1)
不等式 ![]() は直方体Cuboid[pmin,pmax]を表す:
は直方体Cuboid[pmin,pmax]を表す:
行列不等式 (3)
![]() を使って,最小固有値が
を使って,最小固有値が ![]() で最大固有値が
で最大固有値が ![]() の対称行列の集合を定義する.ただし,ℐn=IdentityMatrix[n]かつ κ="SemidefiniteCone"である.これで,固有値が1と2の間にある対称行列の集合
の対称行列の集合を定義する.ただし,ℐn=IdentityMatrix[n]かつ κ="SemidefiniteCone"である.これで,固有値が1と2の間にある対称行列の集合 ![]() (つまり,
(つまり,![]() )が求まる:
)が求まる:
特性と関係 (3)
VectorLessEqualはベクトル空間操作と互換である:
xy は(厳密な意味ではないが)半順序,つまり,反射的,反対称的,推移的である:
テキスト
Wolfram Research (2019), VectorLessEqual, Wolfram言語関数, https://reference.wolfram.com/language/ref/VectorLessEqual.html.
CMS
Wolfram Language. 2019. "VectorLessEqual." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/VectorLessEqual.html.
APA
Wolfram Language. (2019). VectorLessEqual. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VectorLessEqual.html