Norm
Details and Options

- An empty template
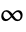 can be entered as
can be entered as 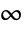 norm
norm , and
, and 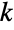 can be entered as
can be entered as 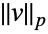 norm2
norm2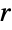 . »
. » - Norm[expr] formats as
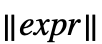 , and Norm[expr,p] formats as
, and Norm[expr,p] formats as 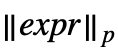 . »
. » - For complex numbers, Norm[z] is Abs[z].
- For vectors, Norm[v] is Sqrt[v.Conjugate[v]]. »
- For vectors, Norm[v,p] is Total[Abs[v]p](1/p) for
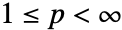 .
. - For vectors, Norm[v,Infinity] is the
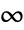 ‐norm given by Max[Abs[v]]. »
‐norm given by Max[Abs[v]]. » - For matrices, Norm[m] gives the spectral or operator norm, which is the maximum singular value of m. »
- Norm specifications for matrices include:
-
1 induced 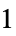 -norm, operator
-norm, operator 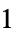 -norm
-norm2 spectral norm, operator norm Infinity induced 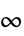 -norm, operator
-norm, operator 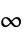 -norm
-norm"Frobenius" Frobenius or Hilbert–Schmidt norm - The
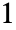 -norm of a matrix is the maximum
-norm of a matrix is the maximum 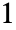 -norm of its columns, whereas the
-norm of its columns, whereas the 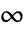 -norm of the matrix is the maximum
-norm of the matrix is the maximum 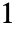 -norm of its rows. »
-norm of its rows. » - The Frobenius norm computes the
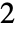 -norm of a vector formed from the entries of the matrix m, i.e Norm[Flatten[m]]. »
-norm of a vector formed from the entries of the matrix m, i.e Norm[Flatten[m]]. » - Norm can be used on SparseArray and structured array objects. »
Examples
open all close allBasic Examples (3)
Scope (16)
Vectors (7)
Matrices (6)
Norm of a matrix, equal to the largest singular value:
Symbolic matrix norm for a real parameter ![]() :
:
When the norm is computed without the assumption of reality, the result is much more complicated:
The ![]() -norm of a matrix is the maximum
-norm of a matrix is the maximum ![]() -norm of the columns of the matrix:
-norm of the columns of the matrix:
The ![]() -norm of a matrix is the maximum
-norm of a matrix is the maximum ![]() -norm of the rows of the matrix:
-norm of the rows of the matrix:
The Frobenius norm for matrices:
All three induced norms of the identity matrix coincide:
The Frobenius norm is distinct, equaling the square root of the dimension:
The spectral norm of a tridiagonal matrix represented as a SparseArray object:
Applications (3)
Estimate the mean distance from the origin to random points in the unit square:
Compare to the asymptotic result:
Solve an ill-conditioned linear system ![]() with a known solution:
with a known solution:
Get the norm of the actual error:
Approximate the solution of ![]() using
using ![]() spatial points and
spatial points and ![]() time steps:
time steps:
Find two solutions with fixed ![]() where the second has twice as many time steps:
where the second has twice as many time steps:
Estimate the error by the norm of the difference:
Extrapolate to a better solution from the first-order convergence of the backward Euler method:
Compute a more accurate solution with NDSolve:
Properties & Relations (7)
The norm is always non-negative:
The norm of v is equal to the square root of the Dot product ![]() :
:
For vectors, the default norm is the 2-norm:
This is also true for matrices:
The limiting value is the ![]() -norm, equal to Max[Abs[v]]:
-norm, equal to Max[Abs[v]]:
The matrix ![]() -norm is the maximum
-norm is the maximum ![]() -norm of m.v for all unit vectors v:
-norm of m.v for all unit vectors v:
This is also equal to the largest singular value of ![]() :
:
The Frobenius norm is the same as the norm of the vector made from the entries of the matrix:
For a matrix m, Norm[m,Infinity] can be computed as Max[Total/@Abs/@m]:
This is equivalent to computing the ![]() -norm of the rows and taking the maximum:
-norm of the rows and taking the maximum:
Norm[m,1] can be computed as Max[Total/@Abs/@Transpose[m]]:
This is equivalent to computing the ![]() -norm of the columns and taking the maximum:
-norm of the columns and taking the maximum:
Possible Issues (2)
It is expensive to compute the ![]() -norm for large matrices:
-norm for large matrices:
If you need only an estimate, the ![]() -norm and
-norm and ![]() -norm are very fast:
-norm are very fast:
Norms of general vectors contain Abs:
Use Simplify and FullSimplify to get simpler answers assuming real parameters:
See Also
Normalize RealAbs Abs EuclideanDistance Dot Total RootMeanSquare ContraharmonicMean SingularValueList Integrate DistanceMatrix
Function Repository: MatrixNorm LogarithmicNorm
Tech Notes
History
Introduced in 2003 (5.0) | Updated in 2025 (14.3)
Text
Wolfram Research (2003), Norm, Wolfram Language function, https://reference.wolfram.com/language/ref/Norm.html (updated 2025).
CMS
Wolfram Language. 2003. "Norm." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/Norm.html.
APA
Wolfram Language. (2003). Norm. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Norm.html
BibTeX
@misc{reference.wolfram_2025_norm, author="Wolfram Research", title="{Norm}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/Norm.html}", note=[Accessed: 27-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_norm, organization={Wolfram Research}, title={Norm}, year={2025}, url={https://reference.wolfram.com/language/ref/Norm.html}, note=[Accessed: 27-February-2026]}

