VertexChromaticNumber

VertexChromaticNumber[g]

gives the chromatic number for the vertices of the graph g.

Details and Options

  • VertexChromaticNumber is also know as chromatic number.
  • VertexChromaticNumber gives the smallest number of colors that can be assigned to the vertices of the graph g such that no two adjacent vertices have the same color.

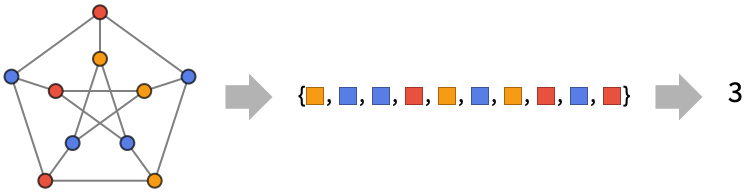
Examples

open allclose all

Basic Examples  (2)

Find a vertex chromatic number of the Petersen graph:

Chromatic numbers of the complete graph:

The formula:

Scope  (6)

VertexChromaticNumber works with undirected graphs:

Directed graphs:

Weighted graphs:

Multigraphs:

Use rules to specify the graph:

VertexChromaticNumber works with large graphs:

Applications  (3)

Making schedules  (1)

A university has a number of different subjects. Each student enrolled in some of these subjects. Build a graph where every vertex is a subject and an edge between two vertices means there is a common student:

Schedule the minimum time slots such that no two exams with a common student are scheduled at same time:

Mobile radio frequency assignment  (1)

When frequencies are assigned to towers, frequencies assigned to all towers at the same location must be different. Build a graph where each vertex is a tower and an edge between two towers represents that they are in range of each other:

Find the minimum number of frequencies needed:

Map coloring  (1)

Build a map where each vertex is an African country and an edge between two countries shows if they are adjacent:

Color the map where any adjacent countries must be assigned a different color:

Find the minimum number of colors:

Properties & Relations  (8)

The chromatic number for a cycle graph is 2 when it has an even number of vertices; otherwise, it is 3:

The chromatic number for a wheel graph is 4 when it has an even number of vertices; otherwise, it is 3:

Bipartite graphs are two-chromatic graphs:

The one-chromatic graphs are empty graphs:

For a graph with vertices and edges, its chromatic number is between 1 and :

:

If a graph contains a clique of size , then its chromatic number is at least :

A graph with vertices, its chromatic number and independence number satisfy :

Use FindVertexColoring to compute VertexChromaticNumber:

Wolfram Research (2021), VertexChromaticNumber, Wolfram Language function, https://reference.wolfram.com/language/ref/VertexChromaticNumber.html.

Text

Wolfram Research (2021), VertexChromaticNumber, Wolfram Language function, https://reference.wolfram.com/language/ref/VertexChromaticNumber.html.

CMS

Wolfram Language. 2021. "VertexChromaticNumber." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/VertexChromaticNumber.html.

APA

Wolfram Language. (2021). VertexChromaticNumber. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VertexChromaticNumber.html

BibTeX

@misc{reference.wolfram_2024_vertexchromaticnumber, author="Wolfram Research", title="{VertexChromaticNumber}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/VertexChromaticNumber.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_vertexchromaticnumber, organization={Wolfram Research}, title={VertexChromaticNumber}, year={2021}, url={https://reference.wolfram.com/language/ref/VertexChromaticNumber.html}, note=[Accessed: 18-November-2024 ]}