WarpingCorrespondence
WarpingCorrespondence[s1,s2]
gives the time warping (DTW) similarity path between sequences s1 and s2.
WarpingCorrespondence[s1,s2,win]
uses a window specified by win for local search.
Details and Options
- WarpingCorrespondence is also known as dynamic time warping.
- WarpingCorrespondence returns {{n1,…,nk},{m1,…,mk}} of nondecreasing positions such that s1〚ni〛 correspond to s2〚mi〛.
- The returned positions attempt to minimize the distance
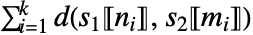over all possible such positions, and with the constraint that all elements of s1 and s2 are represented as some s1〚ni〛 and s2〚mj〛, respectively. - Compute the effective distance using WarpingDistance.
- The sequences si can be lists of numeric or Boolean scalars or vectors.
- Possible settings for the search window win are:
-
Automatic a full search 
r a slanted band window of radius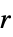 
{"SlantedBand",r} a slanted band window of radius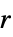 
{"Band",r} band window of radius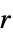 
(Sakoe-Chiba)
{"Parallelogram",a} parallelogram window placed at origin with slopes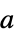 
and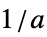 
(Itakura) - A smaller
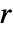typically gives a faster but less optimal result. If ![max(Length[s_1],Length[s_2])<=2 r +1](Files/WarpingCorrespondence.en/13.png "max(Length[s_1],Length[s_2])<=2 r +1")
, then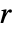 
has no effect. - The following options are supported:
-
DistanceFunction Automatic the distance function to be used Method Automatic the variant of DTW to use - WarpingCorrespondence accepts a DistanceFunctiond option with settings:
-
Automatic automatically determine distance function EuclideanDistance Euclidean distance ManhattanDistance Manhattan or "city block" distance BinaryDistance 0 if elements are equal; 1 otherwise ChessboardDistance Chebyshev or sup norm distance SquaredEuclideanDistance squared Euclidean distance NormalizedSquaredEuclideanDistance normalized squared Euclidean distance CosineDistance angular cosine distance CorrelationDistance correlation coefficient distance BrayCurtisDistance Total[Abs[u-v]]/Total[Abs[u+v]] CanberraDistance Total[Abs[u-v]/(Abs[u]+Abs[v])] MatchingDissimilarity matching dissimilarity between Boolean vectors - By default, the following distance functions are used:
-
EuclideanDistance numeric data MatchingDissimilarity Boolean data - Using Method->Automatic, all elements of s2 are matched with all elements of s1.
- Using Method->{"MatchingInterval"match}, s2 can be matched with a subsequence of s1. Possible settings for match include:
-
Automatic a full match "Flexible" flexible at both ends "FlexibleEnd" flexible only at the end of the interval
Examples
open allclose allBasic Examples (1)
Scope (9)
Data (6)
Search Window (3)
Options (4)
DistanceFunction (3)
With Boolean sequences, WarpingCorrespondence uses MatchingDissimilarity:
Find correspondences between two sequences using different distance functions:
In case of one-dimensional signals, some distance functions are equivalent:
Euclidean, Manhattan, and the chessboard distance are always the same:
Normalized Euclidean distance and correlation distance are the same:
For Boolean data, matching dissimilarity and binary distance are the same:
Applications (2)
Visualize the time warping correspondence by drawing lines between corresponding points:
Compare the first quarter of 2017 of the HPQ stock prices with historical data from 2010 to 2016:
Find the best matching subsequence of historical data:
Detect the historical interval most similar to quarter one of 2017:
Visually compare recent data and the best historical match:
Predict the stock prices for the next 30 days based on historical data:
Properties & Relations (7)
The two sequences need not have the same length:
The warping path of two equal sequences goes along a diagonal line:
Smaller values of the search window radius emphasize speed of computation:
There may be a tradeoff with quality of the computation:
When computing the full correspondence, WarpingCorrespondence is symmetric:
The function is not symmetric when matching subsequences:
Adding to or subtracting from values of one sequence may result in a different correspondence:
Adding to or subtracting from both sequences will not affect the result when distance function is induced by a norm (translation invariant):
This is true for Euclidean, Manhattan, and some more:
Using distance functions that are not translation invariant may produce different correspondence:
Relation with WarpingDistance:
Find the time warped sequences using the correspondence:
WarpingDistance gives the sum of all the distances between corresponding elements:
Text
Wolfram Research (2016), WarpingCorrespondence, Wolfram Language function, https://reference.wolfram.com/language/ref/WarpingCorrespondence.html.
CMS
Wolfram Language. 2016. "WarpingCorrespondence." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WarpingCorrespondence.html.
APA
Wolfram Language. (2016). WarpingCorrespondence. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WarpingCorrespondence.html