WarpingCorrespondence

WarpingCorrespondence[s1,s2]

列 s1と s2のタイムワーピング(DTW)類似性経路を与える．

WarpingCorrespondence[s1,s2,win]

局所探索に win で指定された窓を使う．

詳細とオプション

  • WarpingCorrespondenceは動的タイムワーピングとしても知られている．
  • WarpingCorrespondenceは，s1〚ni〛が s2〚mi〛に対応するような減少しない位置の{{n1,…,nk},{m1,…,mk}}を返す．
  • 返された位置は，そのようなすべての位置で，s1および s2のすべての要素がそれぞれ s1〚ni〛および s2〚mj〛として表されるという制限がある中で，距離を最小にしようとする．
  • WarpingDistanceを使って実質距離を計算する．
  • 列 si は数値あるいはブール値のスカラーあるいはベクトルのリストでよい．
  • 探索窓 win の可能な設定
  • Automatic完全探索
    r半径 の斜め帯窓
    {"SlantedBand",r}半径 の斜め帯窓
    {"Band",r}半径 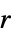の帯窓 (Sakoe-Chiba)
    {"Parallelogram",a}傾斜 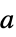と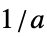 で原点に置かれた平行四辺形窓（板倉）
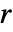  • が小さいほど結果は速く出るが，その最適度は劣る．max(Length[s_1],Length[s_2])<=2 r +1のときは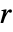， には効果がない．
  • サポートされるオプション
  • DistanceFunction Automatic使用する距離関数
    Method Automatic使用する動的タイムワーピングの異形
  • WarpingCorrespondenceには，次の設定のDistanceFunctiond オプションを使うことができる．
  • Automatic距離関数を自動的に決定する
    EuclideanDistanceユークリッド距離
    ManhattanDistanceマンハッタン距離（「市街地距離」とも呼ばれる）
    BinaryDistance要素が等しい場合は0，それ以外の場合は1
    ChessboardDistanceチェビシェフ(Chebyshev)距離（上限ノルム距離とも呼ばれる）
    SquaredEuclideanDistanceユークリッド距離の二乗
    NormalizedSquaredEuclideanDistanceユークリッド距離の二乗の正規化
    CosineDistance角余弦距離
    CorrelationDistance相関係数距離
    BrayCurtisDistanceTotal[Abs[u-v]]/Total[Abs[u+v]]
    CanberraDistanceTotal[Abs[u-v]/(Abs[u]+Abs[v])]
    MatchingDissimilarityブールベクトル間のマッチング非類似度
  • デフォルトで，次の距離関数が使われる．
  • EuclideanDistance数値データ
    MatchingDissimilarityブールデータ
  • Method->Automaticを使うと，s2の全要素が s1の全要素とマッチされる．
  • Method->{"MatchingInterval"match}を使うと，s2を s1の部分列とマッチすることができる．次は，match の可能な設定である．
  • Automatic完全なマッチ
    "Flexible"両端で柔軟
    "FlexibleEnd"区間の終端でのみ柔軟

例題

すべて開くすべて閉じる

例  (1)

2つの列の間のタイムワーピング対応を求める：

指標間の対応をプロットする：

タイムワープしたバージョンを求める：

ワープしたバージョンはほぼ等しい：

スコープ  (9)

データ  (6)

2つの実数値ベクトル間のタイムワーピング対応を求める：

2つのベクトル列間のタイムワーピング対応を求める：

2つのブールベクトル間のタイムワーピング対応を求める：

ブール値ベクトル列：

互換単位を持つ数量列：

二次元数量配列：

探索窓  (3)

デフォルトで，探索は局所的に制約されない：

探索窓の半径を指定する：

探索半径を2にすると最適のアライメントが求まる：

半径1の帯を使う：

傾き3の平行四辺形を使う：

"Band"窓は，長さが等しい信号については"SlantedBand"窓に等しい：

オプション  (4)

DistanceFunction  (3)

WarpingCorrespondenceは，ブール列についてはMatchingDissimilarityを使う：

2つの列間の対応関係を，異なる距離関数を使って求める：

一次元信号については，距離関数の中に等しいものがある：

ユークリッド距離，マンハッタン距離，チェス盤距離は常に等しい：

正規化されたユークリッド距離と相関距離は等しい：

ブールデータについては，マッチング非類似度とバイナリ距離は等しい：

Method  (1)

完全探索と柔軟な探索の結果を比較する：

結果を可視化して比較する：

アプリケーション  (2)

対応する点の間に線を描くことでタイムワーピング対応を可視化する：

これをあるデータに適用する：

2016年第1四半期のヒューレット・パッカード社(HPQ)の株価を2010年から2016年までのそれと比較する：

過去のデータを入手する：

過去のデータの中で最もよく一致するものを求める：

2017年の第1四半期と最もよく一致する過去の区間を検出する：

最近のデータと最もよく一致する過去のデータを可視化して比較する：

過去のデータに基づいて次の30日間の株価を予測する：

特性と関係  (7)

2つの列が同じ長さである必要はない：

2つの等しい列間のワーピング経路は対角線に沿っている：

探索窓の値が小さいほど計算スピードが上がる：

計算品質とのトレードオフがあるかもしれない：

完全対応を計算するときは，WarpingCorrespondenceは対称である：

部分列をマッチするときは，関数は対称ではない：

1つの列の値に加えたり，そこから除いたりすると，対応関係が変わることがある：

両方の列に加えたり，両方から除いたりしても，距離関数がノルムによって誘発される場合は，結果には影響しない（並進不変）：

以下は，ユークリッド，マンハッタン，その他について真である：

並進不変ではない距離関数を使うと，別の対応関係が与えられるかもしれない：

WarpingDistanceとの関係：

対応関係を使ってライムワープした列を求める：

WarpingDistanceは，対応する要素間のすべての距離の合計を与える：

考えられる問題  (3)

2つの列のすべての要素が同等でなければならない：

2つの列の要素は同じタイプでなければならない：

指定された窓が狭すぎて対応が見付けられない場合には，より大きい窓が自動的に使用される：

Wolfram Research (2016), WarpingCorrespondence, Wolfram言語関数， https://reference.wolfram.com/language/ref/WarpingCorrespondence.html.

テキスト

Wolfram Research (2016), WarpingCorrespondence, Wolfram言語関数， https://reference.wolfram.com/language/ref/WarpingCorrespondence.html.

CMS

Wolfram Language. 2016. "WarpingCorrespondence." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WarpingCorrespondence.html.

APA

Wolfram Language. (2016). WarpingCorrespondence. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WarpingCorrespondence.html

BibTeX

@misc{reference.wolfram_2024_warpingcorrespondence, author="Wolfram Research", title="{WarpingCorrespondence}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/WarpingCorrespondence.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_warpingcorrespondence, organization={Wolfram Research}, title={WarpingCorrespondence}, year={2016}, url={https://reference.wolfram.com/language/ref/WarpingCorrespondence.html}, note=[Accessed: 22-November-2024 ]}