WarpingCorrespondence[s1,s2]
给出序列 s1 与 s2 间的时间翘曲(DTW)相似路径.
WarpingCorrespondence[s1,s2,win]
使用由 win 为局部搜索指定的窗口.


WarpingCorrespondence
WarpingCorrespondence[s1,s2]
给出序列 s1 与 s2 间的时间翘曲(DTW)相似路径.
WarpingCorrespondence[s1,s2,win]
使用由 win 为局部搜索指定的窗口.
更多信息和选项


- WarpingCorrespondence 也被称之为动态时间翘曲.
- WarpingCorrespondence 返回未减少位置的 {{n1,…,nk},{m1,…,mk}},例如 s1〚ni〛 对应于 s2〚mi〛.
- 返回的位置尝试在所有可能的位置上最小化
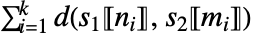 ,在这种约束下, s1 和 s2 的所有元素被分别表示为某种 s1〚ni〛 和 s2〚mj〛.
,在这种约束下, s1 和 s2 的所有元素被分别表示为某种 s1〚ni〛 和 s2〚mj〛. - 使用 WarpingDistance 计算有效的距离.
- 序列 si 可以是数值或布尔标量或向量的列表.
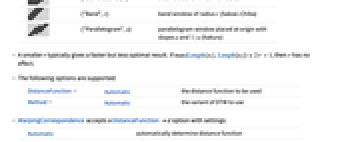
- 搜索窗 win 的可能设置为:
-

Automatic 完整搜索 
r 半径为 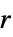 的倾斜带窗
的倾斜带窗
{"SlantedBand",r} 半径为 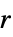 的倾斜带窗
的倾斜带窗
{"Band",r} 半径为 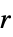 (Sakoe-Chiba) 的倾斜带窗
(Sakoe-Chiba) 的倾斜带窗
{"Parallelogram",a} 放在原点的平行四边形窗,斜率为 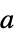 和
和 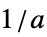 (Itakura)
(Itakura) - 一般
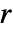 较小,会更快给出结果,但不是最优结果. 如果
较小,会更快给出结果,但不是最优结果. 如果 ![max(Length[s_1],Length[s_2])<=2 r +1 max(Length[s_1],Length[s_2])<=2 r +1](Files/WarpingCorrespondence.zh/13.png) ,那么
,那么 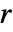 没有任何影响.
没有任何影响. - 支持以下选项:
-
DistanceFunction Automatic 使用的距离函数 Method Automatic 使用 DTW 的变种 - WarpingCorrespondence 接受具有以下设置的 DistanceFunctiond 选项:
-
Automatic 自动确定距离函数 EuclideanDistance 欧几里得距离 ManhattanDistance 曼哈顿或“城区”距离 BinaryDistance 如果元素相等则为 0;否则为 1 ChessboardDistance 切比雪夫或超 (sup) 标准距离 SquaredEuclideanDistance 平方欧几里得距离 NormalizedSquaredEuclideanDistance 正则平方欧几里得距离 CosineDistance 角余弦距离 CorrelationDistance 相关系数距离 BrayCurtisDistance Total[Abs[u-v]]/Total[Abs[u+v]] CanberraDistance Total[Abs[u-v]/(Abs[u]+Abs[v])] MatchingDissimilarity 匹配布尔向量间的相异 - 默认情况下使用以下距离函数:
-
EuclideanDistance 数值数据 MatchingDissimilarity 布尔数据 - 使用 Method->Automatic, s2 的所有元素被 s1 的所有元素匹配.
- 使用 Method->{"MatchingInterval"match},s2 可以用 s1 的子序列匹配. match 的可能设置包括:
-
Automatic 完全匹配 "Flexible" 两端均有弹性 "FlexibleEnd" 只在间隔的一端有弹性
范例
打开所有单元 关闭所有单元范围 (9)
选项 (4)
DistanceFunction (3)
对于布尔序列,WarpingCorrespondence 使用 MatchingDissimilarity:
应用 (2)
属性和关系 (7)
当计算完整响应,WarpingCorrespondence 是对称的:
同时从两个序列增加或减去不会影响结果,当距离函数是由范数(平移不变)产生:
与 WarpingDistance 的关系:
WarpingDistance 给出响应元素间所有距离的总和:
相关指南
-
▪
- 序列调整和比较
文本
Wolfram Research (2016),WarpingCorrespondence,Wolfram 语言函数,https://reference.wolfram.com/language/ref/WarpingCorrespondence.html.
CMS
Wolfram 语言. 2016. "WarpingCorrespondence." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/WarpingCorrespondence.html.
APA
Wolfram 语言. (2016). WarpingCorrespondence. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/WarpingCorrespondence.html 年
BibTeX
@misc{reference.wolfram_2025_warpingcorrespondence, author="Wolfram Research", title="{WarpingCorrespondence}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/WarpingCorrespondence.html}", note=[Accessed: 04-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_warpingcorrespondence, organization={Wolfram Research}, title={WarpingCorrespondence}, year={2016}, url={https://reference.wolfram.com/language/ref/WarpingCorrespondence.html}, note=[Accessed: 04-February-2026]}