WaveletBestBasis[dwd]
computes a best basis representation in the DiscreteWaveletData object dwd.
WaveletBestBasis[dwd,cspec]
computes a best basis representation using the cost specification cspec.


WaveletBestBasis
WaveletBestBasis[dwd]
computes a best basis representation in the DiscreteWaveletData object dwd.
WaveletBestBasis[dwd,cspec]
computes a best basis representation using the cost specification cspec.
Details and Options

- WaveletBestBasis[dwd] returns a DiscreteWaveletData odwd object where the optimal basis has been computed and will be used by functions such as InverseWaveletTransform, WaveletListPlot, etc.
- Properties of the DiscreteWaveletData odwd can be found using odwd["prop"].
- Properties related to best basis include:
-
"BasisIndex" wavelet indices used for inverse transform "BestBasisBlockView" block grid view of best basis "BestBasisCostValues" cost value for each wavelet coefficient "TreeView" tree view of decomposition with best basis highlighted - WaveletBestBasis[dwd] is equivalent to WaveletBestBasis[dwd,"ShannonEntropy"].
- Possible cspec values include:
-
"ShannonEntropy" Shannon entropy 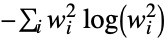
"LogEnergy" log energy 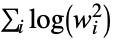
{"Norm",p} norm like ![sum_iTemplateBox[{{w, _, i}}, Abs]^p sum_iTemplateBox[{{w, _, i}}, Abs]^p](Files/WaveletBestBasis.en/3.png) for
for 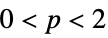 and
and ![-sum_iTemplateBox[{{w, _, i}}, Abs]^p -sum_iTemplateBox[{{w, _, i}}, Abs]^p](Files/WaveletBestBasis.en/5.png) for
for 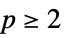
{"Threshold",δ} number of elements above 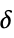
fn apply fn to each coefficient array to get a cost value - A cost function fn must satisfy fn[{a1,…,am,b1,…,bn}]fn[{a1,…,am}]+fn[{b1,…,bn}] and fn[{0,…}]0.
- The best basis is a complete basis for the wavelet decomposition giving the least total cost.
Examples
open all close allBasic Examples (1)
Scope (11)
Basic Uses (6)
Compute an optimal wavelet basis for vector data:
The best basis is stored in the resulting DiscreteWaveletData object:
Show the coefficient array corresponding to each index in the basis:
Wavelet packet transforms give a DiscreteWaveletData object that includes a default basis:
The basis includes all coefficients at the highest level of refinement:
WaveletBestBasis gives a new DiscreteWaveletData object with a different, optimal basis:
Compute best basis for packet transforms with any number of levels of refinement:
Compute wavelet basis, minimizing log-energy for an image:
Compare default basis with best basis in a hierarchical grid layout of coefficient images:
Compute best basis with custom cost function:
Choose basis with fewest coefficients lying between -1 and 1:
Count values lying between -1 and 1 in default basis:
WaveletBestBasis gives the optimal basis among all possible wavelet bases:
Recursively enumerate all possible wavelet bases for ![]() levels of refinement:
levels of refinement:
Show the 5 possible wavelet bases for 2 levels of refinement:
The number of possible bases grows extremely quickly as a function of refinement level:
Distribution of cost values of a random sample of 1000 bases:
Cost Functions (5)
Apply cost functions to coefficients with fixed total energy:
Plot cost as a function of first component energy ![]() for "ShannonEntropy":
for "ShannonEntropy":
In general, each cost function can lead to a different best basis:
Plot distribution of energy among best basis coefficient values for each cost function:
Different cost functions often lead to similar best bases:
Define a custom cost function that favors coefficients that are nearer to integers:
Best basis for list data using custom cost function:
The computed cost value for the {} coefficient is the custom cost value of the original data:
Cost value of the best basis coefficients:
The best basis coefficients are clustered around integers:
Generalizations & Extensions (2)
Applications (3)
Compression (3)
Use WaveletBestBasis to choose a wavelet basis for threshold-based data compression:
Count nonzero values in thresholded coefficients as a measure of compression:
Compare with compression by thresholding original data:
Plot original and reconstructed data:
Compare threshold-based compression for various threshold values ![]() :
:
Use the same threshold value ![]() for best basis selection and thresholding:
for best basis selection and thresholding:
Show reconstructed data along with the number of nonzero values as a measure of compression:
Length of uncompressed original data:
Simple lossy image compression for various threshold values ![]() :
:
Show reconstructed data along with the number of nonzero values as a measure of compression:
Total number of pixel values in all channels of original image:
Properties & Relations (4)
The best basis coefficients typically contain fewer, larger nonzero values than the original data:
Compare default basis for wavelet packet transforms with best basis:
Compare with the basis for non-packet wavelet transforms:
Non-packet transforms give a DiscreteWaveletData object with a permanently fixed basis:
The basis includes the detail coefficients {…,1} and the last coarse coefficient {…,0}:
The result of WaveletBestBasis[dwd] has exactly the same wavelet coefficients as dwd:
Only the wavelet basis is different:
The {} coefficient of "BestBasisCostValues" is the cost value of the original data:
Directly compute log-energy from the data:
The log-energy of the best basis is lower than that of the data:
Possible Issues (5)
DiscreteWaveletTransform does not compute the full tree of wavelet coefficients:
Use DiscreteWaveletPacketTransform to get the full tree:
The cost function must be additive with respect to Join:
The specified function is not additive:
Modify the cost function to be additive:
The cost function must be zero for zero-valued coefficients:
Modify the cost function to be compatible:
The best basis algorithm requires numeric coefficients:
Use specific numerical values:
An explicit basis specification wind needs to be consistent:
A basis cannot include both {1} and {1,0} since {1,0} can be computed from {1}:
Related Guides
History
Text
Wolfram Research (2010), WaveletBestBasis, Wolfram Language function, https://reference.wolfram.com/language/ref/WaveletBestBasis.html.
CMS
Wolfram Language. 2010. "WaveletBestBasis." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WaveletBestBasis.html.
APA
Wolfram Language. (2010). WaveletBestBasis. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WaveletBestBasis.html
BibTeX
@misc{reference.wolfram_2025_waveletbestbasis, author="Wolfram Research", title="{WaveletBestBasis}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/WaveletBestBasis.html}", note=[Accessed: 27-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_waveletbestbasis, organization={Wolfram Research}, title={WaveletBestBasis}, year={2010}, url={https://reference.wolfram.com/language/ref/WaveletBestBasis.html}, note=[Accessed: 27-February-2026]}