WaveletBestBasis
WaveletBestBasis[dwd]
computes a best basis representation in the DiscreteWaveletData object dwd.
WaveletBestBasis[dwd,cspec]
computes a best basis representation using the cost specification cspec.
Details and Options

- WaveletBestBasis[dwd] returns a DiscreteWaveletData odwd object where the optimal basis has been computed and will be used by functions such as InverseWaveletTransform, WaveletListPlot, etc.
- Properties of the DiscreteWaveletData odwd can be found using odwd["prop"].
- Properties related to best basis include:
-
"BasisIndex" wavelet indices used for inverse transform "BestBasisBlockView" block grid view of best basis "BestBasisCostValues" cost value for each wavelet coefficient "TreeView" tree view of decomposition with best basis highlighted - WaveletBestBasis[dwd] is equivalent to WaveletBestBasis[dwd,"ShannonEntropy"].
- Possible cspec values include:
-
"ShannonEntropy" Shannon entropy 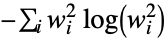
"LogEnergy" log energy 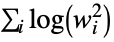
{"Norm",p} norm like ![sum_iTemplateBox[{{w, _, i}}, Abs]^p sum_iTemplateBox[{{w, _, i}}, Abs]^p](Files/WaveletBestBasis.en/3.png) for
for 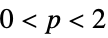 and
and ![-sum_iTemplateBox[{{w, _, i}}, Abs]^p -sum_iTemplateBox[{{w, _, i}}, Abs]^p](Files/WaveletBestBasis.en/5.png) for
for 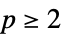
{"Threshold",δ} number of elements above 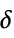
fn apply fn to each coefficient array to get a cost value - A cost function fn must satisfy fn[{a1,…,am,b1,…,bn}]fn[{a1,…,am}]+fn[{b1,…,bn}] and fn[{0,…}]0.
- The best basis is a complete basis for the wavelet decomposition giving the least total cost.
Examples
open allclose allBasic Examples (1)
Scope (11)
Basic Uses (6)
Compute an optimal wavelet basis for vector data:
The best basis is stored in the resulting DiscreteWaveletData object:
Show the coefficient array corresponding to each index in the basis:
Wavelet packet transforms give a DiscreteWaveletData object that includes a default basis:
The basis includes all coefficients at the highest level of refinement:
WaveletBestBasis gives a new DiscreteWaveletData object with a different, optimal basis:
Compute best basis for packet transforms with any number of levels of refinement:
Compute wavelet basis, minimizing log-energy for an image:
Compare default basis with best basis in a hierarchical grid layout of coefficient images:
Compute best basis with custom cost function:
Choose basis with fewest coefficients lying between -1 and 1:
Count values lying between -1 and 1 in default basis:
WaveletBestBasis gives the optimal basis among all possible wavelet bases:
Recursively enumerate all possible wavelet bases for ![]() levels of refinement:
levels of refinement:
Show the 5 possible wavelet bases for 2 levels of refinement:
The number of possible bases grows extremely quickly as a function of refinement level:
Distribution of cost values of a random sample of 1000 bases:
Cost Functions (5)
Apply cost functions to coefficients with fixed total energy:
Plot cost as a function of first component energy ![]() for "ShannonEntropy":
for "ShannonEntropy":
In general, each cost function can lead to a different best basis:
Plot distribution of energy among best basis coefficient values for each cost function:
Different cost functions often lead to similar best bases:
Define a custom cost function that favors coefficients that are nearer to integers:
Best basis for list data using custom cost function:
The computed cost value for the {} coefficient is the custom cost value of the original data:
Cost value of the best basis coefficients:
The best basis coefficients are clustered around integers:
Generalizations & Extensions (2)
Applications (3)
Compression (3)
Use WaveletBestBasis to choose a wavelet basis for threshold-based data compression:
Count nonzero values in thresholded coefficients as a measure of compression:
Compare with compression by thresholding original data:
Plot original and reconstructed data:
Compare threshold-based compression for various threshold values ![]() :
:
Use the same threshold value ![]() for best basis selection and thresholding:
for best basis selection and thresholding:
Show reconstructed data along with the number of nonzero values as a measure of compression:
Length of uncompressed original data:
Simple lossy image compression for various threshold values ![]() :
:
Show reconstructed data along with the number of nonzero values as a measure of compression:
Total number of pixel values in all channels of original image:
Properties & Relations (4)
The best basis coefficients typically contain fewer, larger nonzero values than the original data:
Compare default basis for wavelet packet transforms with best basis:
Compare with the basis for non-packet wavelet transforms:
Non-packet transforms give a DiscreteWaveletData object with a permanently fixed basis:
The basis includes the detail coefficients {…,1} and the last coarse coefficient {…,0}:
The result of WaveletBestBasis[dwd] has exactly the same wavelet coefficients as dwd:
Only the wavelet basis is different:
The {} coefficient of "BestBasisCostValues" is the cost value of the original data:
Directly compute log-energy from the data:
The log-energy of the best basis is lower than that of the data:
Possible Issues (5)
DiscreteWaveletTransform does not compute the full tree of wavelet coefficients:
Use DiscreteWaveletPacketTransform to get the full tree:
The cost function must be additive with respect to Join:
The specified function is not additive:
Modify the cost function to be additive:
The cost function must be zero for zero-valued coefficients:
Modify the cost function to be compatible:
The best basis algorithm requires numeric coefficients:
Use specific numerical values:
An explicit basis specification wind needs to be consistent:
A basis cannot include both {1} and {1,0} since {1,0} can be computed from {1}:
Text
Wolfram Research (2010), WaveletBestBasis, Wolfram Language function, https://reference.wolfram.com/language/ref/WaveletBestBasis.html.
CMS
Wolfram Language. 2010. "WaveletBestBasis." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WaveletBestBasis.html.
APA
Wolfram Language. (2010). WaveletBestBasis. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WaveletBestBasis.html