WaveletBestBasis
WaveletBestBasis[dwd]
DiscreteWaveletDataオブジェクト dwd の最良基底表現を計算する.
WaveletBestBasis[dwd,cspec]
コスト指定 cspec を使って最良基底表現を計算する.
詳細とオプション

- WaveletBestBasis[dwd]はDiscreteWaveletData odwd オブジェクトを返す.このオブジェクトでは最適化基底が計算されておりInverseWaveletTransform,WaveletListPlot等の関数で使用される.
- DiscreteWaveletData odwd の特性は odwd["prop"]を使って求めることができる.
- 最良基底関連特性
-
"BasisIndex" 逆変換に使用されるウェーブレット指標 "BestBasisBlockView" 最良基底のブロック格子ビュー "BestBasisCostValues" 各ウェーブレット係数の費用値 "TreeView" 最良基底をハイライトした分解のツリービュー - WaveletBestBasis[dwd]はWaveletBestBasis[dwd,"ShannonEntropy"]に等しい.
- 使用可能な cspec の値
-
"ShannonEntropy" Shannonエントロピー 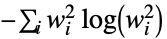
"LogEnergy" 対数エネルギー 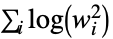
{"Norm",p} 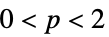 では
では![sum_iTemplateBox[{{w, _, i}}, Abs]^p sum_iTemplateBox[{{w, _, i}}, Abs]^p](Files/WaveletBestBasis.ja/4.png) ,
,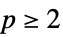 では
では![-sum_iTemplateBox[{{w, _, i}}, Abs]^p -sum_iTemplateBox[{{w, _, i}}, Abs]^p](Files/WaveletBestBasis.ja/6.png) のようなノルム
のようなノルム{"Threshold",δ} 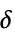 を超える要素数
を超える要素数fn fn を各係数配列に適用して費用値を得る - 費用関数 fn は fn[{a1,…,am,b1,…,bn}]fn[{a1,…,am}]+fn[{b1,…,bn}]と fn[{0,…}]0を満足しなければならない.
- 最良基底は最小総費用を与えるウェーブレット分解の完全基底である.
例題
すべて開くすべて閉じるスコープ (11)
基本的な用法 (6)
最良基底は結果のDiscreteWaveletDataオブジェクトに保存されている:
ウェーブレットパケット変換はデフォルト基底を含むDiscreteWaveletDataオブジェクトを与える:
この基底には最高の細分化レベルにおけるすべての係数が含まれている:
WaveletBestBasisは,別の最適化基底を持つ新たなDiscreteWaveletDataオブジェクトを与える:
画像の対数エネルギーを最小化してウェーブレット基底を計算する:
係数画像の階層的な格子レイアウトでデフォルト基底を最良基底と比較する:
WaveletBestBasisは他のすべての可能なウェーブレット基底の中の最適化基底を与える:
一般化と拡張 (2)
アプリケーション (3)
圧縮 (3)
WaveletBestBasisを使って閾値に基づいたデータ圧縮のウェーブレット基底を選ぶ:
再構築されたデータを圧縮尺度としての非零値の数とともに示す:
特性と関係 (4)
最良基底係数に含まれる非零の値の数は一般にもとのデータに含まれる非零の値よりも少ないがそれぞれの値は大きい:
ウェーブレットパケット変換のデフォルト基底を最良基底と比較する:
非パケット変換は永久に修正された基底を持つDiscreteWaveletDataオブジェクトを与える:
この基底は詳細化係数{…,1}と最後の粗い係数{…,0}を含む:
WaveletBestBasis[dwd]の結果は dwd と完全に等しいウェーブレット係数を持つ:
考えられる問題 (5)
DiscreteWaveletTransformはウェーブレット係数の完全木は計算しない:
DiscreteWaveletPacketTransformを使って完全木を得る:
費用関数はJoinを使った際に加算可能でなければならない:
テキスト
Wolfram Research (2010), WaveletBestBasis, Wolfram言語関数, https://reference.wolfram.com/language/ref/WaveletBestBasis.html.
CMS
Wolfram Language. 2010. "WaveletBestBasis." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WaveletBestBasis.html.
APA
Wolfram Language. (2010). WaveletBestBasis. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WaveletBestBasis.html