WaveletBestBasis[dwd]
计算在 DiscreteWaveletData 对象 dwd 中的最优基表示.
WaveletBestBasis[dwd,cspec]
使用代价指定 cspec 计算最优基表示.


WaveletBestBasis
WaveletBestBasis[dwd]
计算在 DiscreteWaveletData 对象 dwd 中的最优基表示.
WaveletBestBasis[dwd,cspec]
使用代价指定 cspec 计算最优基表示.
更多信息和选项

- WaveletBestBasis[dwd] 返回一个 DiscreteWaveletData odwd 对象,其中已经对最优基进行计算,并且将被诸如 InverseWaveletTransform、WaveletListPlot 等函数使用.
- DiscreteWaveletData odwd 的属性可以使用 odwd["prop"] 求得.
- 与最优基相关的属性包括:
-
"BasisIndex" 用于逆变换的小波的小波索引 "BestBasisBlockView" 最优基的块状网格视图 "BestBasisCostValues" 每个小波系数的代价值 "TreeView" 分解的树状视图,其中突出显示最优基 - WaveletBestBasis[dwd] 等价于 WaveletBestBasis[dwd,"ShannonEntropy"].
- 可能的 cspec 值包括:
-
"ShannonEntropy" 香农熵 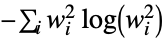
"LogEnergy" 对数能量 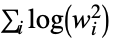
{"Norm",p} 范数,对于 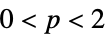 类似
类似 ![sum_iTemplateBox[{{w, _, i}}, Abs]^p sum_iTemplateBox[{{w, _, i}}, Abs]^p](Files/WaveletBestBasis.zh/4.png) ,并且对于
,并且对于 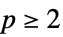 类似
类似 ![-sum_iTemplateBox[{{w, _, i}}, Abs]^p -sum_iTemplateBox[{{w, _, i}}, Abs]^p](Files/WaveletBestBasis.zh/6.png)
{"Threshold",δ} 超过 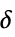 的元素数目
的元素数目fn 将 fn 应用于系数数组以获取一个代价值 - 一个代价函数 fn 必须满足 fn[{a1,…,am,b1,…,bn}]fn[{a1,…,am}]+fn[{b1,…,bn}] 和 fn[{0,…}]0.
- 最优基是小波分解中给出最低总体代价的完全基.
范例
打开所有单元 关闭所有单元范围 (11)
基本用途 (6)
最优基存储在所得的 DiscreteWaveletData 对象中:
小波包变换给出包含一个默认基的 DiscreteWaveletData 对象:
WaveletBestBasis 给出一个具有不同的最优基的新的 DiscreteWaveletData 对象:
WaveletBestBasis 给出所有可能的小波基中的最优基:
应用 (3)
压缩 (3)
使用 WaveletBestBasis 来选择基于阈值的数据压缩的小波基:
属性和关系 (4)
非包变换给出具有永久固定基的一个 DiscreteWaveletData 对象:
WaveletBestBasis[dwd] 的结果具有与 dwd 完全相同的小波系数:
可能存在的问题 (5)
DiscreteWaveletTransform 不计算小波系数组成的完全树:
使用 DiscreteWaveletPacketTransform 以获取完全树:
代价函数必须是关于 Join 可加的:
相关指南
-
▪
- 小波分析
文本
Wolfram Research (2010),WaveletBestBasis,Wolfram 语言函数,https://reference.wolfram.com/language/ref/WaveletBestBasis.html.
CMS
Wolfram 语言. 2010. "WaveletBestBasis." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/WaveletBestBasis.html.
APA
Wolfram 语言. (2010). WaveletBestBasis. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/WaveletBestBasis.html 年
BibTeX
@misc{reference.wolfram_2025_waveletbestbasis, author="Wolfram Research", title="{WaveletBestBasis}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/WaveletBestBasis.html}", note=[Accessed: 18-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_waveletbestbasis, organization={Wolfram Research}, title={WaveletBestBasis}, year={2010}, url={https://reference.wolfram.com/language/ref/WaveletBestBasis.html}, note=[Accessed: 18-February-2026]}