WaveletThreshold
WaveletThreshold[dwd]
在 DiscreteWaveletData 对象 dwd 中对细节小波系数求阈值.
WaveletThreshold[dwd,tspec]
使用阈值指标 tspec 对系数求阈值.
WaveletThreshold[dwd,tspec,wind]
对由小波索引 wind 给出的小波系数求阈值.
更多信息



- WaveletThreshold[dwd] 等效于 WaveletThreshold[dwd,"Universal"].
- WaveletThreshold[dwd,tspec,wind] 表明对哪个小波系数求阈值,使用与 DiscreteWaveletData 一样的索引规范.
- 默认情况下,在每个精细度层上求阈值.
- 阈值指标 tspec 的形式为:tfun, {tfun,pars}.
- 可能的 tfun 名称和选项包括:
-
{"Hard",δ} ![0 TemplateBox[{x}, Abs]<=delta; x TemplateBox[{x}, Abs]>delta 0 TemplateBox[{x}, Abs]<=delta; x TemplateBox[{x}, Abs]>delta](Files/WaveletThreshold.zh/1.png)
{"Soft",δ} ![ 0 TemplateBox[{x}, Abs]<=delta; sgn(x) (TemplateBox[{x}, Abs]-delta) TemplateBox[{x}, Abs]>delta; 0 TemplateBox[{x}, Abs]<=delta; sgn(x) (TemplateBox[{x}, Abs]-delta) TemplateBox[{x}, Abs]>delta;](Files/WaveletThreshold.zh/2.png)
{"Firm",δ,r,p} ![ 0 TemplateBox[{x}, Abs]<=delta-delta p r; (sgn(x) (delta+delta r-delta p r) (TemplateBox[{x}, Abs]-delta+delta p r))/(delta r) delta-delta p r<TemplateBox[{x}, Abs]<=delta+delta (-p) r+delta r; x TemplateBox[{x}, Abs]>delta+delta (-p) r+delta r; 0 TemplateBox[{x}, Abs]<=delta-delta p r; (sgn(x) (delta+delta r-delta p r) (TemplateBox[{x}, Abs]-delta+delta p r))/(delta r) delta-delta p r<TemplateBox[{x}, Abs]<=delta+delta (-p) r+delta r; x TemplateBox[{x}, Abs]>delta+delta (-p) r+delta r;](Files/WaveletThreshold.zh/3.png)
{"PiecewiseGarrote",δ} ![0 TemplateBox[{x}, Abs]<=delta; x-(delta^2)/x TemplateBox[{x}, Abs]>delta 0 TemplateBox[{x}, Abs]<=delta; x-(delta^2)/x TemplateBox[{x}, Abs]>delta](Files/WaveletThreshold.zh/4.png)
{"SmoothGarrote",δ,n} 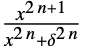
{"Hyperbola", 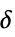 }
}![ 0 TemplateBox[{x}, Abs]<=delta; sgn(x) sqrt(x^2-delta^2) TemplateBox[{x}, Abs]>delta; 0 TemplateBox[{x}, Abs]<=delta; sgn(x) sqrt(x^2-delta^2) TemplateBox[{x}, Abs]>delta;](Files/WaveletThreshold.zh/7.png)
{"LargestCoefficients",k} 保持最大的 k 系数 - 在所有情况下,
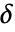 假设为正数或用阈值函数 tfunc 计算
假设为正数或用阈值函数 tfunc 计算 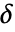 . 每个 tfunc[coefi,windi] 应该返回一个正数.
. 每个 tfunc[coefi,windi] 应该返回一个正数. - "Firm" 的参数条件为
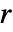 是正实数,
是正实数,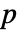 是0和1间的正实数.
是0和1间的正实数. - "SmoothGarrotte" 的参数条件是
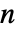 为正实数.
为正实数. - 阈值
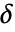 可以用以下方法自动进行计算:
可以用以下方法自动进行计算: -
Automatic "Universal" 阈值 {"FDR",α} 在显著性级别 α 上的错误发现率 "GCV" 最小化广义交叉验证函数 "GCVLevel" 每一级执行的"GCV" "SURE" Stein 的无偏风险估计 "SUREHybrid" "SURE" 和 "Universal" 阈值的组合 "SURELevel" 每一级执行的"SURE" "Universal" Donoho 和 Johnstone 的通用阈值 "UniversalLevel" 每一级执行的"Universal" - {"FDR",α} 的参数条件为:α 是位于0到1之间的数. "FDR" 默认等价于 {"FDR",0.05}.
- 可以使用以下简短的 tspec 形式:
-
"FDR" {"Soft",{"FDR",0.05}} "GCV" {"Soft","GCV"} "GCVLevel" {"Soft","GCVLevel"} "SURE" {"Hard","SURE"} "SURELevel" {"Hard","SURELevel"} "SUREShrink" {"Soft","SURE"} "Universal" {"Hard","Universal"} "UniversalLevel" {"Hard","UniversalLevel"} "VisuShrink" {"Soft","Universal"} "VisuShrinkLevel" {"Soft","UniversalLevel"}
范例
打开所有单元关闭所有单元基本范例 (2)
噪声数据的 DiscreteWaveletTransform:
使用 InverseWaveletTransform 合成平滑图像,与原始图像相比较:
范围 (12)
基本用途 (4)
WaveletThreshold 操作于一个 DiscreteWaveletData 对象:
结果是一个表示阈值系数的新的 DiscreteWaveletData 对象:
使用 WaveletListPlot 进行比较:
使用 Automatic 对逆变换中的系数求阈值:
使用 All 所有系数求阈值:
推广和延伸 (1)
使用 FindThreshold 计算阈值:
应用 (8)
基准阈值方法 (2)
计算阈值 (3)
使用 WaveletThreshold 计算 "Universal" 阈值:
使用 WaveletThreshold 计算 "SURE" 阈值:
使用 WaveletThreshold 计算 "FDR" 阈值:
属性和关系 (9)
对于小的阈值 ![]() ,阈值函数接近于 Identity:
,阈值函数接近于 Identity:
"Hard" 阈值类似于 Chop:
低于某个阈值 ![]() 的数据值被设为0;高于
的数据值被设为0;高于 ![]() 的数据值被
的数据值被 ![]() “收缩”:
“收缩”:
参数 ![]() (
(![]() ) 控制 Firm 阈值插值在 0 和 Identity 间的范围. 参数
) 控制 Firm 阈值插值在 0 和 Identity 间的范围. 参数 ![]() (
(![]() ) 控制位于
) 控制位于 ![]() 和
和 ![]() 间的
间的 ![]() ,默认情况下,
,默认情况下,![]() :
:
"Firm" 阈值是 "Hard" 与 "Soft" 阈值的折中:
"Firm" 阈值比 "Hard" 阈值具有更小的均匀偏差:
在极限 ![]() ,"SmoothGarotte" 成为 "Hard" 阈值:
,"SmoothGarotte" 成为 "Hard" 阈值:
使用 WaveletMapIndexed 执行 "Hard" 阈值:
可能存在的问题 (3)
文本
Wolfram Research (2010),WaveletThreshold,Wolfram 语言函数,https://reference.wolfram.com/language/ref/WaveletThreshold.html.
CMS
Wolfram 语言. 2010. "WaveletThreshold." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/WaveletThreshold.html.
APA
Wolfram 语言. (2010). WaveletThreshold. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/WaveletThreshold.html 年