ZernikeR
ZernikeR[n,m,r]
gives the radial Zernike polynomial ![]() .
.
Details
- Mathematical function, suitable for both symbolic and numerical manipulation.
- Explicit polynomials are given when possible.
- The Zernike polynomials are orthogonal with weight
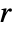 over the unit interval.
over the unit interval. - ZernikeR can be evaluated to arbitrary numerical precision.
- ZernikeR automatically threads over lists.
- ZernikeR can be used with Interval and CenteredInterval objects. »
Examples
open allclose allBasic Examples (4)
Scope (26)
Numerical Evaluation (6)
The precision of the output tracks the precision of the input:
Evaluate efficiently at high precision:
ZernikeR can be used with Interval and CenteredInterval objects:
Compute the elementwise values of an array:
Or compute the matrix ZernikeR function using MatrixFunction:
Specific Values (3)
Visualization (3)
Plot the ZernikeR function for various orders:
Function Properties (10)
Domain of ZernikeR of integer orders:
The range for ZernikeR of integer orders:
ZernikeR has the mirror property ![]() :
:
ZernikeR is an analytic function of x:
ZernikeR is neither non-decreasing nor non-increasing:
ZernikeR is not injective:
ZernikeR is neither non-negative nor non-positive:
ZernikeR has no singularities or discontinuities:
ZernikeR is neither convex nor concave:
TraditionalForm formatting:
Differentiation (2)
Applications (1)
Properties & Relations (6)
Obtain a sequence of Zernike polynomials from their generating function:
Compare with the directly computed sequence:
Verify the differential equation satisfied by the Zernike polynomial:
Verify recurrence relations satisfied by Zernike polynomials:
An integral representation of the radial Zernike polynomial:
Compare with the result of ZernikeR:
ZernikeR can be represented in terms of MeijerG:
Radial Zernike polynomials are orthogonal on the unit interval with weight function ![]() :
:
Text
Wolfram Research (2007), ZernikeR, Wolfram Language function, https://reference.wolfram.com/language/ref/ZernikeR.html.
CMS
Wolfram Language. 2007. "ZernikeR." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ZernikeR.html.
APA
Wolfram Language. (2007). ZernikeR. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ZernikeR.html