WOLFRAM

Wolfram Language & System Documentation Center
"PolynomialResult" (Comparison Method)

"PolynomialResult" (Comparison Method)

Compare mathematical expressions in a way suitable for exercises about polynomials, allowing reordering of factors but no other computation.

Details

  • The polynomial comparison method only considers two polynomials to be equivalent if they are equal and they are factored into the same terms. Expanded forms are not considered equivalent to factored forms.
  • The values of the key and answer can both be specified as held expressions Hold[expr] to maintain the values exactly as they were given. Even when the values are held, reordering transformations are performed to determine equivalence during assessment, but no computation is allowed.
  • Values in "PolynomialResult" answer keys are patterns and support Blank expressions.
  • By default, answers are considered correct even if terms are differently ordered or negative signs and numeric coefficients are differently distributed.
  • The setting "DistributedCoefficients" determines whether polynomials differing only by numeric coefficients are considered equivalent. For example, by default 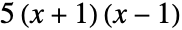and 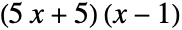are considered equivalent.
  • In AssessmentFunction[key,<|"ComparisonMethod""PolynomialResult","DistributedCoefficients"setting|>], the following values are supported for setting:
  • All (default)any equivalently numeric coefficient is marked correct
    "Sign"equivalent distributions of –1 are marked correct
    Nonecoefficients and signs must exactly match the answer key
  • The following tables show comparisons of "PolynomialResult" with other comparison methods for typical answer keys and several possible submitted answers:

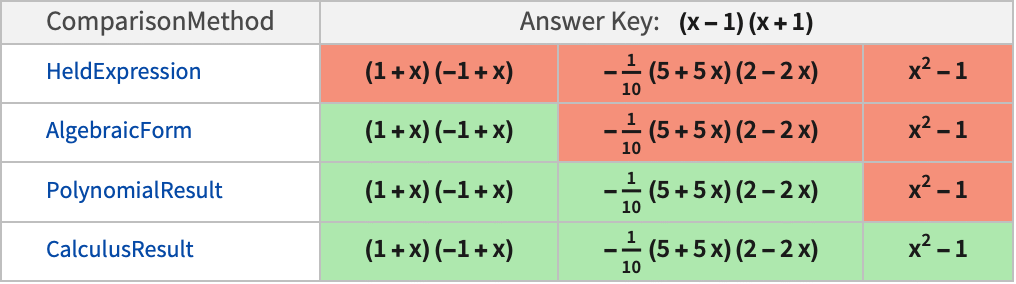
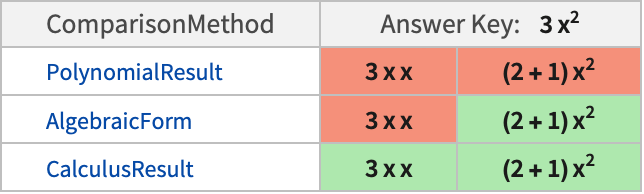
Examples

open all close all

Basic Examples  (1)

Create an AssessmentFunction for a polynomial question:

Use it to assess an answer:

The expanded form of the same polynomial is not considered correct:

Scope  (6)

Create an assessment function for the question "Expand the polynomial (x+y)^2(x-y)^2":

Supplying the original question is not considered correct:

Equivalent polynomials that differ by reordering are considered correct:

Polynomials differing by arithmetic are considered different:

Polynomials differing only by placement of negative signs are considered equivalent:

Specify the comparison method using an Association:

By default, equivalent distributions of numeric coefficients are marked as correct:

Require coefficients to match the answer key exactly:

The distributed form is marked incorrect:

The factored form with terms in any order is marked correct:

Allow only differently distributed signs:

Moving the negative sign to any term is allowed:

Distributing the coefficient is not allowed:

Generalizations & Extensions  (1)

Create a polynomial QuestionObject:

Attempting to provide the solution as code will give an incorrect answer:

Applications  (1)

Include multiple patterns in an assessment function, awarding more points for each correct coefficient:

Try many values:

Properties & Relations  (6)

Arbitrary operations are not performed in held answers:

Global definitions of variables are ignored during assessment:

If two polynomials are equal but differently factored, the "PolynomialResult" comparison method will give an incorrect assessment:

The "CalculusResult" comparison method will give a correct assessment:

Define a polynomial assessment including a constant coefficient:

Answers are considered correct for any factoring of the coefficient:

Define a pattern for a polynomial with two arbitrary coefficients:

Create an AssessmentFunction using the pattern:

Any answer matching the pattern is marked as correct:

Use Blank[] patterns for coefficients. Correct answers can differ by these coefficient values as well as signs and a single constant coefficient:

Factorized and expanded forms are considered not equivalent: