WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター
"PolynomialResult" (比較法)

"PolynomialResult" (比較法)

多項式の問題に適した方法で数式を比較する．因数の並べ替えは許容されるが，その他の計算は許容されない．

詳細

  • 多項式比較法は，2つの多項式が等しくかつ同じ項に因数分解されている場合にのみ，この2つの多項式が等しいとみなす．展開された形は因数分解された形と等しいとはみなされない．
  • 解答集と答の値はどちらも，厳密に与えられた値を保持するためにホールドされた式 Hold[expr]として指定できる．たとえ値がホールドされていても，評価中に等価性を決定するために変換の並べ替えは行われるが，計算は許されない．
  • "PolynomialResult"の解答集における値はパターンで，Blank式をサポートする．
  • デフォルトで，項の順序が違ったり負の符号や数値係数の順序が異なっていても答は正解であるとみなされる．
  • "DistributedCoefficients"の設定は，数値係数だけが異なる多項式を同等とみなすかどうかを決定する．例えば，デフォルトで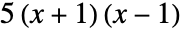と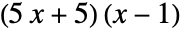は等価であるとみなされる．
  • AssessmentFunction[key,<|"ComparisonMethod""PolynomialResult","DistributedCoefficients"setting|>], では，setting に対して次の値がサポートされている．
  • All （デフォルト）数値的に等しい任意の係数は正解とマークされる
    "Sign"–1の同等な配置は正解とマークされる
    None係数と符号は解答集と厳密に一致しなければならない
  • 次の表は，一般的な解答集の解と提出された可能性のあるいくつかの解答について，"PolynomialResult"と他の比較方法との比較を示している．

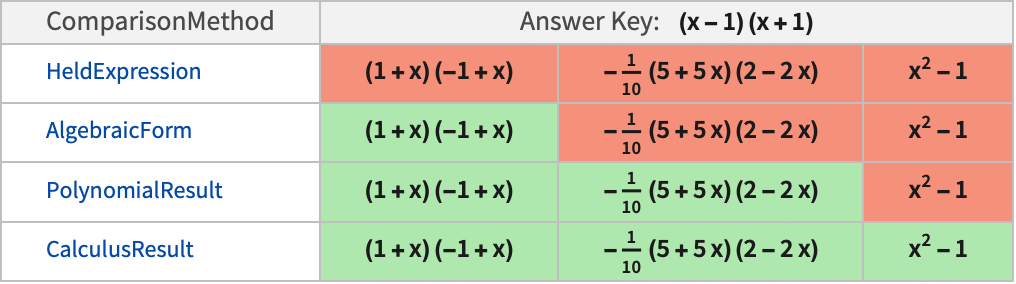
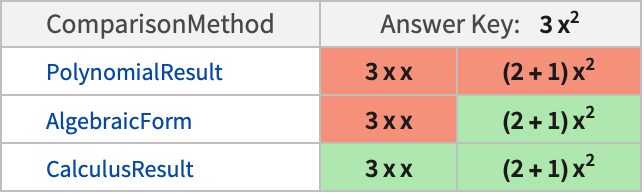
例題

すべて開く すべて閉じる

例  (1)

多項式の問題についてのAssessmentFunctionを作成する：

これを使って答を評価する：

同じ多項式の展開した形は正しいとはみなされない：

スコープ  (6)

「Expand the polynomial (x+y)^2(x-y)^2」という問題に対する評価関数を作成する：

もとの問題を与えても正しいとはみなされない：

並べ方を変えた同等の多項式は正しいとみなされる：

算術的に異なる多項式は異なるとみなされる：

負の符号の配置だけが異なる多項式は同等であるとみなされる：

Associationを使って比較方法を指定する：

デフォルトで，係数の同等の配置は正解とマークされる：

係数が解答集と厳密に一致することが必要であるとする：

配布された形式は不正解とマークされる：

因数分解された形は，項の順序にかかわらず，正解とマークされる：

符号の配置が異なるもののみが許される：

負の符号を任意の項に動かすことは許される：

係数を配布することは許されない：

一般化と拡張  (1)

多項式のQuestionObjectを作成する：

解をコードとして与えようとすると正しくない答が与えられる：

アプリケーション  (1)

評価関数に複数のパターンを含める．正しい係数ごとにより多くの点を付与する：

多くの値を試す：

特性と関係  (6)

任意の操作はホールドされた答の中では実行されない：

変数の大域定義は評価中は無視される：

2つの多項式が等しくはあるが因数分解の仕方が異なっている場合，"PolynomialResult"比較法は正しくない答を与える：

"CalculusResult"比較法は正しい評価を与える：

定数係数を含む多項式の評価を定義する：

答は，係数の任意の因数分解について正しいとみなされる：

任意の2つの係数がある多項式のパターンを定義する：

このパターンを使ってAssessmentFunctionを作成する：

パターンと一致する答はどれも正解である：

Blank[]パターンを係数に使う．これらの係数の値，符号，単一の定数係数が違っていても正解である：

因数分解と展開の形式は同等とはみなされない：